CLASS-1
ADDITION THROUGH BUILDING BLOCK
ADDITION THROUGH BUILDING BLOCK
Addition through building block is another way to get understand about logic of addition, details with logic through example is given below -
ADDITION OF TWO NUMBERS BY BUILDING BLOCKS -
Addition through building blocks is a method of teaching addition to young children using physical objects or manipulatives. It helps them understand the concept of adding numbers by visually representing the process.
Here's a simple explanation of how addition through building blocks works:
- Gather building blocks or any small objects that can be easily manipulated, such as cubes or counters. Assign a specific value to each block, for example, one block represents the number 1.
- Start with two numbers you want to add, for instance, 3 and 4. Take three blocks representing the first number (3) and place them in a row or stack. Then take four blocks representing the second number (4) and place them next to the first row or stack.
- Count all the blocks together to find the sum. In this case, you would count all the blocks in the row or stack, which would give you a total of 7 blocks.
- Explain to the child that the sum of 3 and 4 is equal to 7, and that the blocks represent the numbers being added.
- Repeat this process with different numbers to help the child grasp the concept of addition. You can also experiment with different arrangements of the blocks, such as making a tower with one number and adding blocks to it.
By physically manipulating the blocks and seeing the visual representation of addition, children can better understand how numbers combine to form a sum. This hands-on approach can make addition more concrete and engaging for young learners. As children become comfortable with addition through building blocks, they can transition to mental math and symbolic representations of addition.
Addition through building blocks is a mathematical concept that helps visualize and understand the process of adding numbers. It involves breaking down the numbers into smaller units or "building blocks" and then combining them to find the sum.
To illustrate addition through building blocks, let's consider an example:
Let's say we want to add 3 and 4 using building blocks. We can represent each number using individual blocks. Here, we can use small cubes as building blocks, with each cube representing the value of 1.
Representing 3 : o o o
Representing 4 : o o o o
To find the sum, we can combine the blocks from both numbers:
o o o o o o o
Counting all the blocks together, we have a total of 7 blocks. Therefore, 3 + 4 = 7.
This visual representation using building blocks can help children or individuals who are learning addition to understand the concept by physically manipulating and combining the blocks. It provides a concrete and tangible way to grasp the abstract idea of addition.
This method can also be extended to larger numbers by using more building blocks. For example, to add 17 and 9, you would represent 17 with 17 blocks and 9 with 9 blocks. Then, you combine them to find the total number of blocks, representing the sum.
This approach is a useful tool for teaching addition, especially at the elementary level, as it helps develop number sense and a deeper understanding of the mathematical operation.
Addition can be understood and visualized using building blocks or units. Let's consider the example of adding 3 and 5:
Suppose there are two different number of two different colors of blocks one is ‘Red’ another is ‘Green’, and also let there are 5 no.s ‘Red’ blocks and 3 no.s ‘Green’ blocks.
Step 1: Start with three building blocks to represent the number 3.
Step 2: Add five more building blocks to represent the number 5.
Step 3: Combine the two sets of building blocks together.
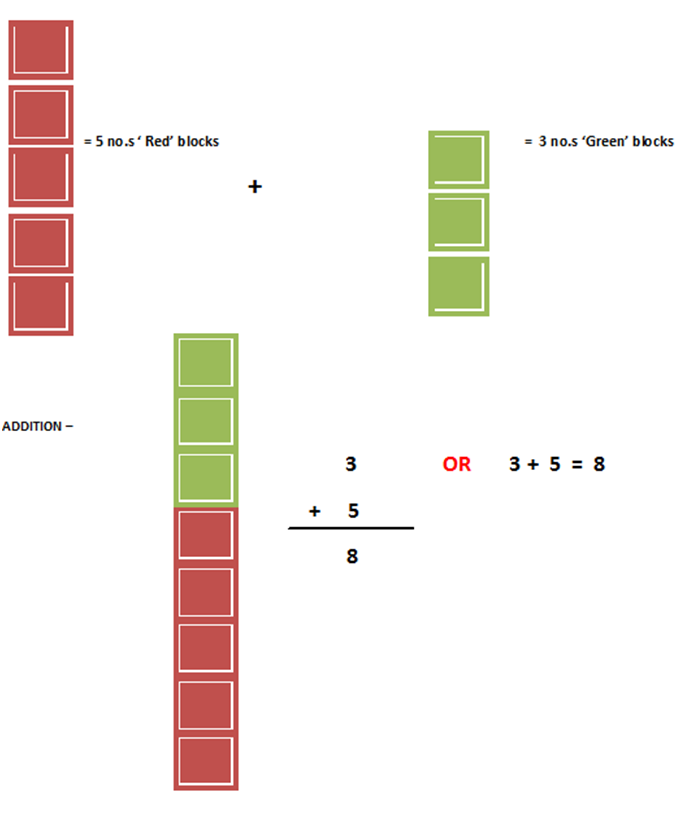
Step 4: Count the total number of building blocks. In this case, there are eight blocks, which represents the sum of 3 and 5.
So, 3 + 5 = 8.
This visual representation with building blocks demonstrates the process of combining two quantities together to find their sum. You can use the same approach for adding any two single-digit numbers.
When you mention "addition through building block," I assume you're referring to a method of performing addition by using a building block or a modular approach. This approach breaks down the addition process into smaller steps or components, allowing you to build up to the final sum.
Here's a simple example of addition through building blocks using base-10 numbers:
- Start by aligning the numbers you want to add vertically, with the units digit (rightmost digit) lined up.
- Begin with the rightmost digits and add them together. If the sum is less than 10, write it down as the rightmost digit of the result. If it's equal to or greater than 10, write down only the units digit and carry the tens digit to the next column.
- Move to the next column to the left and add the digits in that column, including any carry from the previous step.
- Repeat this process for each column, moving from right to left, until you've added all the digits.
- If there are no more columns to add and you have a carry remaining, write it down as an additional digit to the left of the final result.
Here's an example to illustrate the process:
2 3 4 5
+ 1 6 8 2
-------------
4 0 2 7
Step 1: Align the numbers vertically.
2 3 4 5
+ 1 6 8 2
-------------
? ? ? ?
Step 2: Add the rightmost digits (5 + 2 = 7).
2 3 4 5
+ 1 6 8 2
--------------
7
Step 3: Add the next column (4 + 8 = 12). Write down 2 and carry 1.
2 3 4 5
+ 1 6 8 2
--------------
2 7
Step 4: Add the next column (3 + 6 + 1 = 10). Write down 0 and carry 1.
2 3 4 5
+ 1 6 8 2
--------------
0 2 7
Step 5: Add the leftmost column (2 + 1 = 3). Since there are no more columns to add, we're done.
2 3 4 5
+ 1 6 8 2
------------------
4 0 2 7
So, by breaking down the addition process into smaller steps or building blocks, you can perform addition more easily and accurately.