CLASS-9
VOLUME & SURFACE OF THE SOLID - PROBLEM & SOLUTION

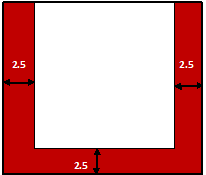
So, the internal length would be = [125 – (2.5 X 2)] = 120 cm

Now, the internal breadth would be = [105 – (2.5 X 2)] = 100 cm

And, the internal depth would be = [90 – 2.5] = 87.5 cm

So, the capacity of the said cistern would be = volume of the cuboid

                       = (l X b X h) cubic units

                      = (120 X 100 X 87.5) cm³                                                                                                                                  (120 X 100 X 87.5)

                    = ------------------- liters = 1050 liters …………(i)

                               1000

(ii) Volume of iron = External volume – Internal volume

                 = [(125 X 105 X 90) – (120 X 100 X 87.5)]

                 = [1181250 – 1050000] cm³ = 131250 cm³.......(ii)

(iii) External area = Area of 4 faces + Area of the base

                    = [2(l + b) X h] + (l X b)  cm²

                    = [2(125 + 105) X 90] + (125 X 105) cm²

                    = (41400 + 13125) cm² 

                    =  54525 cm²

Internal area = Area of 4 faces + Area of the base

               = [2(l + b) X h] + (l X b)  cm²

               = [2(120 + 100) X 87.5] + (120 X 100) cm²

               =  (38500 + 1200) cm²

               =  50500  cm²

Area at the top = Area between outer and inner rectangles

                  = [(125 X 105) – (120 X 100)]  cm²

                  =  (13125 – 12000) cm²

                  =  1125 cm²

Now, the total surface area = (54525 + 50500 + 1125) cm²

                               =  106150 cm² ............(iii)     (Ans.)

Example.3) A field is 70 m long and 60 m broad. In one corner of the field , a pit which is 10 m long, 5 m broad, and 6 m deep has been dug out. The earth taken out of it is evenly spread over the remaining part of the field. Find the rise in the level of the field.

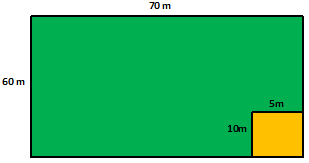
Area of the field = (70 X 60) m² = 4200 m²

Area of the pit = (10 X 5) m² = 50 m²

Area over which the earth is spread out = (4200 – 50) m² = 4150 m²

Volume of the earth drug out = (l X b X h)

                                 = (10 X 5 X 6) = 300 m³

                        Volume

So, Rise in level = (----------)

                         Area

                          300 m³           300 m

                   = (-----------) = (----------)

                         4150 m²           4150

                        300 X 100

                   = (------------) cm            (Ans.)

                           4150

Example.4) Total surface area of a cube is 864 cm². Find its volume.

Ans.) Let the side of the cube be ‘a’ cm

So, as per the formulae, its total surface area = (6a²) cm²

So, 6a² = 864

Or, a² = 144

Or, a = √144 = √12² = 12 cm

Now, the volume of the cube = a³ cm³

                                = (12 X 12 X 12) cm³

                                = 1728 cm³    (Ans.)

Example.5) A room is half as long again as it is broad. The cost of carpeting the room at $ 18 per m³ is $ 972 and the cost of white washing the four walls at $ 6 per m² is $ 1080. Find the dimensions of the room.

Ans.) Let breadth = (a) m

                    3a

Then, length = (------) m

                     2

Let, height of the room = y m

                           Cost of carpeting          972

Area of the floor = (-------------------) = (-------) m²=  

                                Rate                   18

                                                  = 54 m²

Now, as the formula of area of rectangular

                            = (length X breadth) sq.Units

            3a

    So, ------- X a = 54

            2

        3a²

Or, ------- = 54

         2

              54 X 2

Or,  a² = --------- = 36

                3

Or,   a² = 36 = 6²

Or,   a = √6² =  6

                                      3a          3

So, breadth = 6 m and length = (-----) = (----- X 6) = 9 m

                                       2          2

                                 Cost of white washing

Now, area of four walls = (----------------------)

                                         Rate

                               1080

                          = (-------) m² = 180 m²

                                 6

So, as per the formulae = [2 (l + b) X h]

                           = [2 (6 + 9) X y] = 30y

As per the given condition, 30y = 180

                          Or,  y = 6

Hence, length = 6 m, breadth = 9 m, height = 6 m.      (Ans.)

Example.6) The water in a rectangular reservoir having a base 80 m X 60 m, 6.5 m deep. In what time can water be emptied by a pipe of which the cross section is a square of side 20 cm, if water runs through the pipe at the rate of 15 km/hr ?

Ans.)  Volume of water in the reservoir = (l X b X h)

                                            = (80 X 60 X 6.5) m³

                                            = 31200 m³

                                      20         20              1

Area of cross section of pipe = (------ X ------) m² = ------ m²

                                     100        100             25

                                            1

Volume of water emptied in 1 hour = (----- X 15000) m³ = 600 m³

                                           25

                                            31200

Time taken to empty the reservoir = (---------) hrs = 52 hrs   (Ans.)

                                             600