CLASS-9
VOLUME & SURFACE AREA OF THE SOLIDS -DIAGONAL OF CUBOID
DIAGONAL OF CUBOID -
Cuboid – A rectangular solid bounded by six rectangular plane faces is called a cuboid. A match box, a chalk box, a brick, a block, a book, etc., are all examples of a cuboid. A cuboid has 6 rectangular faces, 12 edges and 8 vertices. Let us considered a cuboid of length = l units, breadth = b units, and height = h units.
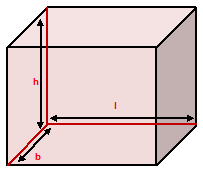
Diagonal of a Cuboid –
The line joining (red color) opposite corners of a cuboid is called its diagonal. A cuboid has four diagonals. A diagonal of a cuboid is the length of the longest rod that can be placed in the cuboid.
Diagonal of cuboid = √l² + b² + h² units
Example.) Find the length of the longest rod that can be placed in a room 15 m long, 16 m broad, and
2
10 ------ m high.
3
2 32
Ans.) Here, l = 15 m, b = 16 m, h = 10 ------ = ------- = 10.67 m
3 3
Length of the longest rod = Length of Diagonal
= √l² + b² + h²
= √(15)² + (16)² + (10.67)²
= √225 + 256 + 113.85
= √594.85 = 24.4 m (Ans.)