CLASS-9
TRIGONOMETRICAL RATIOS - TWO DIMENSIONAL PROBLEMS
Two-Dimensional Problems –
Example.1) A light post 15 m long rest against a vertical wall at an angle of 60⁰ with the ground.
Calculate – (i) how high up the wall will the pole reach.
(ii) how far is the foot of the pole from the wall.
Ans.)
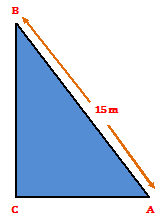
Let AB be the light post, resting against the wall CB. Let AC denote the horizontal ground. Then, AB = 15 m and ∠CAB = 60⁰.
(i) from right △ACB, we have
CB
-------- = sin 60⁰
AB
CB √3
Or, ------- = ------
15 2
15√3
Or, CB = ------- m
2
Hence the pole reaches (15√3)/2 m high up the wall. (Ans.)
(ii) from right △ACB, we have –
AC
------- = cos 60⁰
AB
AC 1
Or, ------- = ------
15 2
15
Or, AC = ------- m = 7.5 m
2
Hence, the foot of the pole is at a distance of 7.5 m from the wall. (Ans.)
Example.2) A vertically straight tree, 20 m high, is broken by the wind in such a way that its top touches the ground and makes an angle of 60⁰ with the ground. At what height from the ground did the tree break ? (take √3 = 1.73)
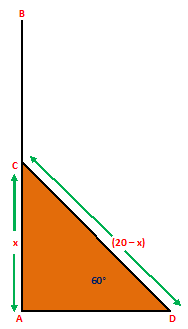
Ans.) Let AB be the tree broken at a point C and the part CB, taking the position CD, meeting the ground at D.
Let, AC = x meters.
Then, CB = (20 – x) m
So, CD = CB = (20 – x) m,
and ∠ADC = 60⁰
From right △DAC, we have
AC
------- = sin 60⁰
CD
x √3
Or, ---------- = -------
(20 – x) 2
Or, 2 x = √3 (20 – x)
Or, 2 x = 20√3 - √3 x
Or, 2 x + √3 x = 20√3
Or, 2 x + 1.73 x = (20 X 1.73)
Or, 3.73 x = 34.6
34.6
Or, x = -------- = 9.28 m = 9.3 m
3.73
Hence, the tree broke at a height of 9.3 m from the ground. (Ans.)
Example.3) The string of a kite is 150 m long and it makes an angle of 45⁰ with the horizontal. Find the height of the kite from the ground. (take √2 = 1.14)
Ans.) Let AB be the string of the kite and AC be the horizontal. Then, AB = 150 m and ∠CAB = 45⁰.
Now, from right △ACB, we have –
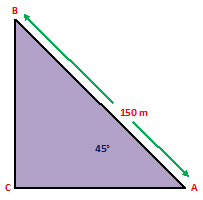
CB
-------- = sin 45⁰
AB
CB 1
Or, -------- = ------
150 √2
150
Or, CB = -------- = 75 √2
√2
Or, CB = (75 X 1.41) = 105.75 m
Hence, the kite is at a height of 105.75 m from the ground. (Ans.)
Example.4) An electric people is 15 m high. A steel wire tie to the top of the pole is affixed at a point on the ground to keep the pole upright. The steel wire makes an angle of 30⁰with the horizontal, through the foot of the pole. Find the length of the steel wire.
Ans.) Let AC be the steel wire and BC be the pole.
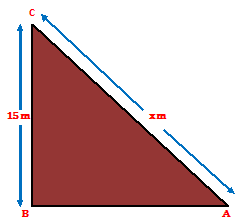
Then, AB is the horizontal. Let, AC = x meters.
So, BC = 15 m, and ∠BAC = 30⁰.
From, right △ABC, we have –
BC
------- = sin 30⁰
AC
15 1
Or, ------- = ------
x 2
Or, x = 15 X 2 = 30 m
Hence, the length of the wire is 30 m. (Ans.)