CLASS-9
TRIGONOMETRICAL RATIO - SQUARE RELATIONS IN T-RATIOS
Square Relations in T-Ratios -
Theorem-2. In a right angled triangle, for any acute angle θ, we have :-
(i) sin² θ + cos² θ = 1,
(ii) 1 + tan² θ = sec² θ,
(iii) 1 + cot² θ = cosec² θ
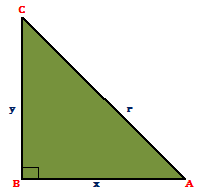
Proof : - Consider a right angled △ABC in which ∠B = 90⁰ and ∠A = θ⁰
Let, AB = x units, BC = y units, AC = r units
Then, by the Pythagoras theorem, we have - x² + y² = r²
Y X
(i) sin² θ + cos² θ = (-----)² + (-----)²
r r
y² x²
= (------ + ------)
r² r²
(y² + x²) r²
= ------------ = ------- [x² + y² = r²] = 1
r² r²
So, sin² θ + cos² θ = 1 (Proved)
y
(ii) 1 + tan² θ = 1 + (-----)²
x
y² x² + y²
= 1 + ------ = ----------- [x² + y² = r²]
x² x²
r² r
= ------ = (-----)² = sec² θ
x² x
1 + tan² θ = sec² θ (Proven)
x
(iii) 1 + cot² θ = 1 + (------)²
y
x² y² + x²
= 1 + ------- = ---------- [x² + y² = r²]
y² y²
r² r
= --------- = (--------)² = cosec² θ (Proved)
y² y