CLASS-9
PROBLEM & SOLUTION OF CROSS MULTIPLICATION - SIMULTANEOUS LINEAR EQUATIONS

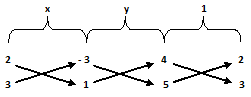
             x                       y                          1

=> ---------------- = ----------------- = -----------------

    (2 X 1) – {3 X (-3)}      {(-3) X 5} – (1 X 4)       (4 X 3) – (5 X 2)

            x                       y                      1

=> --------------- = --------------- = ----------------  

          2 + 9                -15 – 4                12 – 10

          x                  y                1

=> ----------- = ------------ = ----------

         11               -19                2

Hence,  x = 11/2, and y = -19/2 is the required solution.  (Ans.)

Example.2) Solve the system of equations 2x – 3y = 12, 3x + 2y = - 5 by the method of cross multiplications.

Ans.)  The given equations are –

        2x – 3y = 12

=>   2x – 3y – 12 = 0 ………………………..(i)

And,   3x + 2y = - 5

=>   3x + 2y + 5 = 0  …………………..(ii)

By cross multiplication, we have –

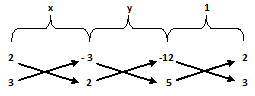
                     x                         y                        1

=> ----------------- = ------------------ = ----------------

      (2 X 2) – {3 X (-3)}       {(-3) X 5} – {(-12) X 2}    {(-12) X 3} – (5 X 2)}

          x                    y                    1

=> ------------ = -------------- = --------------

        4 + 9            - 15 + 24           - 36 – 10

         x              y              1

=> --------- = --------- = ----------

        13             9            - 46

Hence, x = - 13/46, and y = - 9/46 is the required solution.  (Ans.)

                                                                                                                               5           2

Example.3) solve the system of equations ------- - ------ + 1 = 0,  

                                               x + y       x – y                       

     15             7

 --------- + -------- = 10 ( x≠y )

    x + y         x – y

Ans.)   Equations given –

        5              2

   --------- - --------- + 1 = 0 ........................ (i) 

      x + y          x – y

       15              7

  ---------- + --------- = 10  ........................ (ii)

      x + y          x – y

                 1                          1

Let,  u  = ----------,  and  v = ---------- we get -

               x + y                     x – y

     5u – 2v + 1 = 0 ...................(iii)

    15u + 7v – 10 = 0.....................(iv)

By cross multiplication, we have –

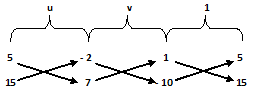
                    u                        v                          1

=> ---------------- = ----------------- = -----------------

     (5 X 7) – {15 X (-2)}      {(-2) X (-10)} – (1 X 7)      (1 X 15) – {(-10) X 5)}

           u                     v                      1

=> ------------- = --------------- = ---------------

      (35 + 30)             (20 – 7)              (15 + 50)

         u                v               1

=> ---------- = ---------- = ----------

        65              13              65

Or,   u = 1

Replacing, x + y = 1

So,   x + y – 1 = 0 ………………….. (v)

And,   v  = 1/5

Replacing,  x – y = 5

So,  x – y – 5 = 0 …………………….(vi)

By cross multiplication, we have –

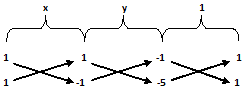
                      x                        y                        1

=> ----------------- = ----------------- = -----------------

      {1 X (-1)} – (1 X 1)     {1 X (-5)} – {(-1) X (-1)}   {(-1) X 1} – {1 X (-5)}

           x                     y                      1

=> ------------- = --------------- = ----------------

       (-1 – 1)              (-5 – 1)               (-1 + 5)

          x                 y                 1

=> ----------- = ------------ = -----------

       - 2               - 6                 4

So, x = (-2)/4  = - 1/2

And, y = (-6)/4 = - 3/2

Hence, x = - 1/2, and y = - 3/2 is the required solution.   (Ans.)