CLASS-9
CIRCUMFERENCE & AREA OF THE CIRCLE - PROBLEM & SOLUTION

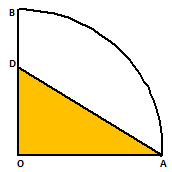
We have –

                       1                        1

Area of △OAD = ------ X OA X OD = (------ X 3.5 X 2) cm²

                       2                        2

                               1

Area of quadrant OAB = ------ πr²

                               4

       1          22          7          7

 = (------ X ------ X ------ X ------)

       4           7          2          2

      77

 = ------ cm² =  9.625 cm²

      8

Area of unshadded or uncolured portion

              = (Area of quadrant OAB) – (Area of △OAD)

              =  (9.625 – 3.5) cm²

              =  6.125 cm²

soo, the area of unshadded portion is 6.125 cm² (Ans.)

Example.2) ABC is an isosceles triangle with ∠ABC = 90⁰, A semi circle s drawn with AC as diameter. If AB = BC = 7 cm, find the area of the shaded region . (Taken π = 22/7)

Ans.)   

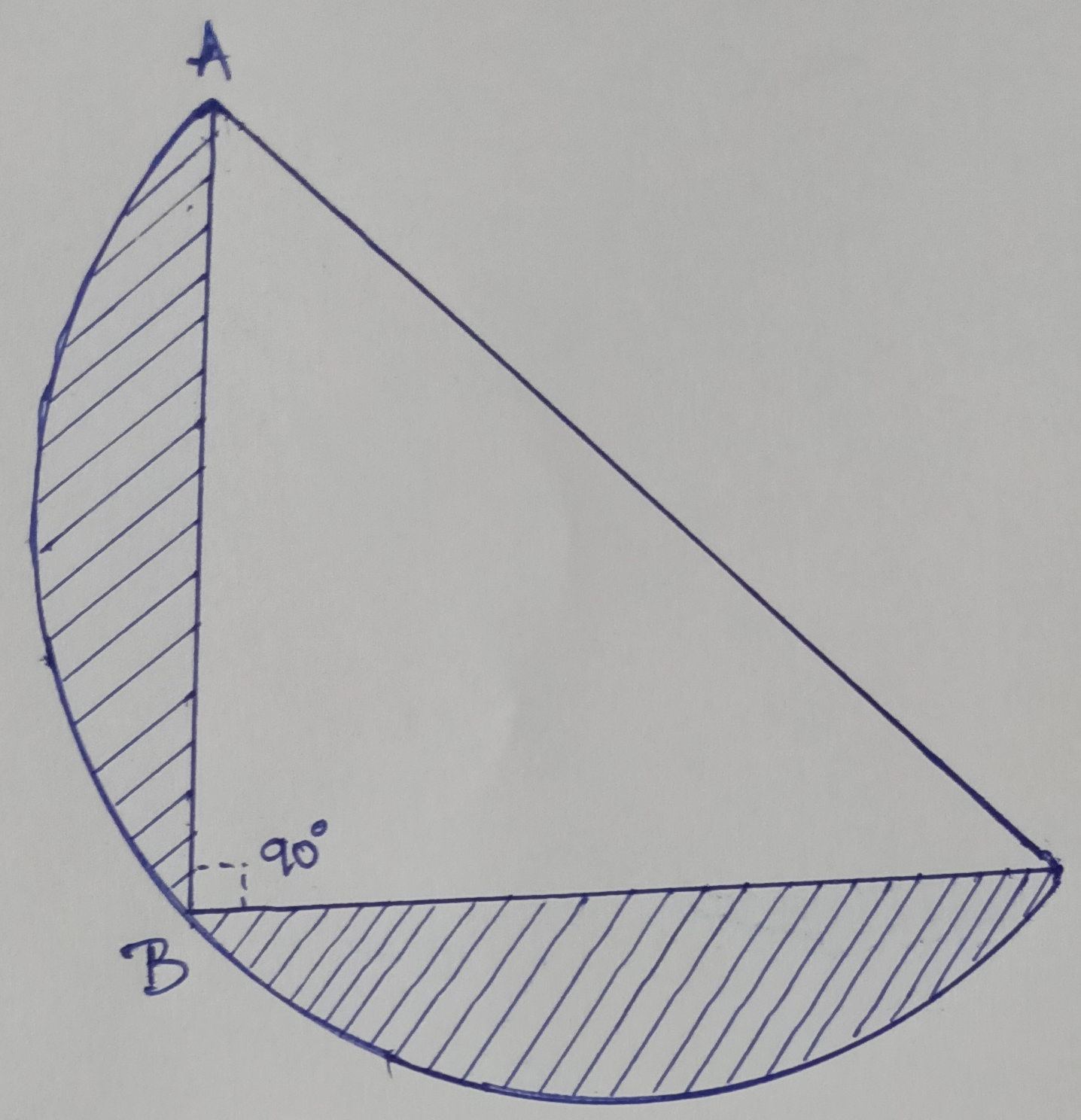
                          1

Area of △ABC = (-----X AB X BC)

                       2

                      1                          49

                = (------ X 7 X 7) cm² = ------- cm²

                      2                           2       

Now, AC² = AB² + BC²

            = 7² + 7² = 49 + 49 = 98

           AC  = √98 = 7√2 cm

                                     AC          7√2            7

Radius of the semi-circle (R) = ------- = ------- cm = ------ cm

                                      2            2             √2

                               1

Area of the semi circle = ----- πR²

                               2

                      1         22         7

               =  {----- X ------ X (-----)²}  cm²

                      2         7          √2

                   77

               = ----- cm²

                    2

Area of shadded region = (Area of semi circle) – (Area of △ABC)

                                77         49

                           = (------ - ------) cm² 

                                 2          2

                                28

                           = ------ cm² = 14 cm²       (Ans.)

                                2

Example.3) A doorwayis decorated as shown in the figure, there are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. centres of three equal semi-circles lie on BC. ABC is isosceles triangle with AB = AC. If BO = OC, find the area of the shadded region. (take π = 22/7)

Ans.)  

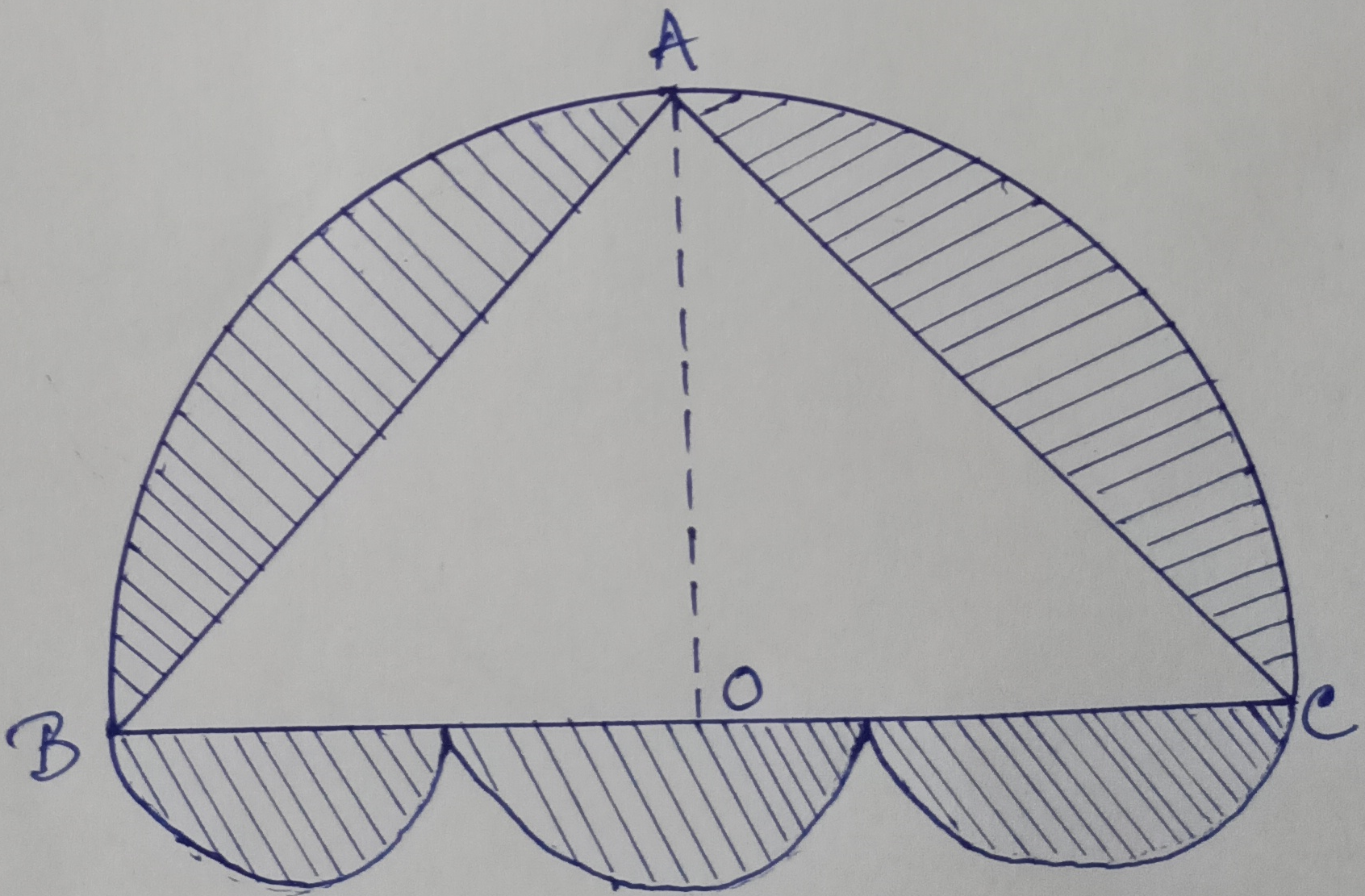
Join OA.

       BC = 84 cm

=>    OB = OC = 42 cm

Radius of larger circle (R) = 42 cm

Sum of diameters of 3 small semi circles = 84 cm

So, diameter of the each small semi circle = 84/3 cm = 28 cm

Radius of each small semi-circle (r) = 28/2 = 14 cm

Also,  ∠AOB = ∠AOC = 90ᵒ

                                   1

Area of larger semi-circle = ------ (πR²)

                                   2

                 1          22

          =  (------ X ------ X 42 X 42) cm² = 2772 cm²

                 2          7

                                                  1    

Area of each of the smaller semi-circles = ----- (πr²)

                                                  2

                                                                                     1          22

=  (------ X ------ X 14 X 14) cm² = 308 cm²

       2          7

Area of 3 smaller semi-circles = (308 X 3) cm² = 924 cm²

Area of △ABC = 1/2 X BC X OA = 1/2 X 84 X 42 = 1764 cm²

Area of shadded Region = (Area of large semi-circle) + (Area of 3 smaller semi-circles) – (Area of △ABC)

                          = (2772 + 924 – 1764) cm²

                          = (3696 – 1764) cm² = 1932 cm²

Hence, the area of shadded region 1932 cm²      (Ans.)

Example.4) In the given figure, a circle circumscribes a rectangle with sides 12 cm & 9 cm. Calculate –

(i) The Circumference of the Circle to nearest cm

(ii) The area of the shadded Region, Correct to 2 places of Decimal in cm². Take π = 3.14

Ans.)  

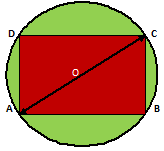
Let ABCD be the rectangle with AB = 12 cm, and BC = 9 cm

So,  AC² = AB² + BC²

Or,  AC = √(AB² + BC²) = √(12² + 9²)

                            = √(144 + 81) = √225 = 15 cm

Let, ‘O’ be the midpoint of AC. Then ‘O’ is the center and OA the radius of the circum circle.

So, radius OA = AC/2 = 15/2 = 7.5 cm 

So, now the circumference of the circle = 2πr

                                 = (2 X 3.14 X 7.5)  [π = 3.14 given]

                                 = 47.1 cm

Hence, the circumference of the circle, correct to nearest cm is 47 cm ............(i)        (Ans.)

The area of the green region is

                           = (Area of the circle) – (Area of the rectangle)

                           =  πr²- (l X w)

                           =  [(3.14 X 7.5 X 7.5) – (12 X 9)]

                           =  (176. 625 – 108) cm²

                           =  68.625 cm²

                           =  68.63 cm²      

The area of the shadded region, correct to 2 decimal places in cm² is 68.63 cm² ...................(ii)   (Ans.)