CLASS-9
CIRCUMFERENCE & AREA OF A CIRCLE - INTRODUCTION & FORMULAE
CIRCUMFERENCE & AREA OF CIRCLE –
For every circle circle, the ratio between the circumference and diameter in a constant. This constant is represented by a Greek letter π (Pi)
Circumference
So, π = -----------------
Diameter
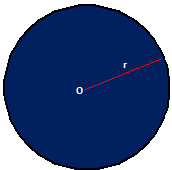
1. For a circle of radius = r units, we have -
(i) Circumference of the circle
= 2πr units = πd units
Where d is the parameter, and d = 2r
(ii) Area of a circle = πr² sq.units
2. For a semi circle of radius = r units, we have –
1
(i) Area of the semi-circle = ------- πr² sq.units
2
(ii) Perimeter of a semi-circle = (πr + 2r) units
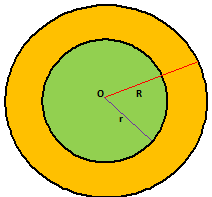
3. Area of a Circular Ring –
If R & r be the outer and inner radii of a ring, then
Area of the ring = π (R²- r²) sq.units
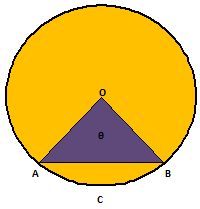
4. Results on Sectors &
Segments –
Suppose an arc ACB makes an angle θᵒ at the center O of a circle of
2πrθ
(i) Length of arc ACB = (---------) units
360
πr²θ
(ii) Area of Sector OACBO = (-------) units
360
1 2πrθ
= ------ X r X (--------) sq.units
2 360
1
= (------ X radius X arc length) sq.units
2
(iii) Perimeter of the Sector OACBO= length of the arc ACB + OA + OB
2πrθ
= (------- + 2r) units
360
5. Rotation Made by an wheel –
(i) Distance moved by a wheel in 1 revolution
= Circumference of the Wheel
(ii) Number of rotations made by a wheel in unit time
Distance moved by it in unit time
= --------------------------------
Circumference of the wheel
6. Facts about Clocks :
(i) Angle described by minute hand in 60 minutes = 360ᵒ
360
(ii) Angle described by minute hand in 5 minutes = (------ X 5) = 30ᵒ
60
(iii) Angle described by hour hand in 12 hours = 360ᵒ
Angle described by hour hand in 1 hour = 30ᵒ
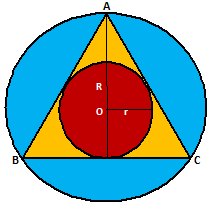
7. Equilateral Triangle -
In a equilateral triangle of side a units, we have
√3a
(i) Height of the triangle, h = ------ units
2
√3a²
(ii) Area of the Triangle = (------) sq.units
4
(iii) Radius of incircle, r = h/3 = (a/2√3) units
(iv) Radius of circumcircle, R = 2h/3 = (a/√3) units
Thus, r = a/2√3 and R = a/√3