CLASS-9
CIRCUMFERENCE & AREA OF CIRCLE - EQUILATERAL TRIANGLE
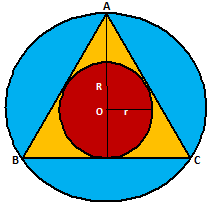
EQUILATERAL TRIANGLE -
In a equilateral triangle of side a units, we have
√3a
(i) Height of the triangle, h = ------- units
2
√3a²
(ii) Area of the Triangle = (------) sq.units
4
(iii) Radius of Incircle, r = h/3 = (a/2√3) units
(iv) Radius of Circumcircle, R = 2h/3 = (a/√3) units
Thus, r = a/2√3 and R = a/√3
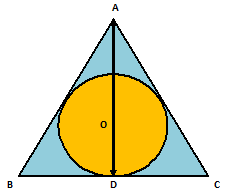
Example.1) In an equilateral triangle of side 24 cm, a circle is inscribed, touching its sides. Find the area of the remaining portion of the triangle. Take √3 = 1.73 and π = 3.14
Ans.) Let △ABC be the given equilateral triangle in which a circle is inscribed.
Side of the Triangle, a = 24 cm
√3 √3
Height of the triangle, h = (------ X a) = (------ X 24) = 12√3 cm
2 2
1 1
Radius of the incircle, r = ------ h = ----- X 12√3 cm = 4√3 cm
3 3
Required area = Area of the shaded region
= (Area of the △ABC) – (Area of incircle)
√3
= [(------ a²) – (πr²)
4
√3
= [{(------ X 24 X 24) – {3.14 X (4√3)²}] cm²
4
= [(√3 X 6 X 24) – (3.14 X 48)] cm²
= (144√3 – 150.72) cm²
= [(1.73 X 144) – 150.72] cm²
= (249.12 – 150.72) cm²
= 98.4 cm²
so, area of the remaining portion of the triangle is 98.4 cm² (Ans.)
Example.2) The figure shows a running track surrounding a grass enclosure PQRSTU. The enclose consist of a rectangle PQST with a semi circular region at each end. Given, PQ = 200m and PT = 70m
(i) Calculate the area of grassed enclosure in m²
(ii) Given that the track is of constant width 7m, calculate the outer perimeter ABCDEF of the track.
Ans.)
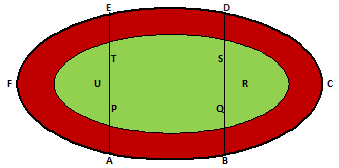
Ans.) Diameter of each semicircular region of grassed enclosure = PT = 70 m
Radius of each one of them = 35 m.
Area of grassed enclosure –
= (Area of Rect. PQST) + 2 (Area of semi-circular region with radius 35 m)
1
= (PQ X PT) + 2 X ------ πr²
2
22
= [(200 X 70) + ------ X 35 X 35] m²
7
= 17850 m² …………………………………………………(i) (Ans.)
Diameter of each outer semi-circle of the track
= AE = (PT + 7 + 7) m = 84 m
So, radius of each one of them = 42 m
Outer perimeter ABCDEF = (AB + DE + Semi-circle BCD + Semi-circle EFN)
= (2PQ + 2 X circumference of the semi-circle with radius 42 m)
= {(2 X 200) + (2 X π X 42)} m
22
= {400 + (2 X ------- X 42)} m
7
= {400 + (12 X 22)} m = (400 + 264) m
= 664 m ……………………………(ii) (Ans.)