CLASS-9
AREA OF CIRCULAR RING
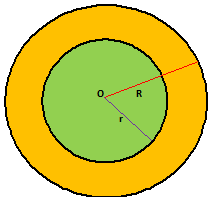
AREA OF A CIRCULAR RING -
If R & r be the outer and inner radii of a ring, then
Area of the ring = π (R² - r²) sq.units
Example.1) The area enclosed by the circumference of two concentric circles is 346.5 cm². If the circumference of the inner circle is 132 cm, calculate the radius of the outer circle.

Ans.) Let the radius of inner circle be r cm.
Then, its circumference = 2πr cm
So, as per the given condition
Or, 2πr = 132
22
Or, 2 X ------- X r = 132
7
132 X 7
Or, r = ----------- = 21 cm
2 X 22
Let the radius of the outer circle be R cm.
Then, the area of the ring = (πR² - πr²) cm²
= π (R² - r²)
= π (R² - 21²)
As per the given condition, π (R²- 21²) = 346.5
22
=> ------- (R²- 441) = 346.5
7
346.5 X 7
=> (R²- 441) = ------------ = 110.25
22
=> R² = 110.25 + 441 = 551.25
=> R = √551.25 = 23.48 cm
Hence the radius of the outer circle is 23.48 cm (Ans.)
Example.2) Two circles touch externally. Sum of their areas is 130π sq. Cm and the distance between their centers is 14 cm. Determine the radii of the circles
Ans.) Let the radii of the given circles be R cm & r cm respectively. As the circles touches externally, distance between their centers = (R + r) cm
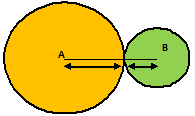
From the above picture –
R + r = 14 .......................(i)
Sum of their areas = (πR² + πr²) cm² = π (R² + r²) cm²
According to the given condition –
π (R² + r²) = 130 π
or, R² + r² = 130 .......................(ii)
we have the identity, (R + r)² + (R – r)² = 2(R² + r²)
now, we will substitute the value of (i) & (ii), and we get –
Or, (14)²+ (R – r)² = 2 X 130 [from (i) & (ii)]
Or, 196 + (R – r)² = 260
Or, (R – r)² = 64 = 8²
Or, (R – r) = 8 ...................(iii)
Now, we will add (i) & (iii), and we get –
R + r = 14
R – r = 8
--------------
2 R = 22
Or, R = 11
Now, we will substitute the value of R in (i) and we get –
R + r = 14
Or, 11 + r = 14
Or, r = 3
So, the radii of the circles are 11 cm & 3 cm respectively. (Ans.)
Example.3) Two circles touches internally. The sum of their areas is 116π sq cm and the distance between their centers in 6 cm. Find the radii of the gives circles.
Ans.) Let the radii of the given circles be R cm and r cm respectively.
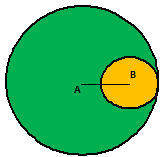
As the circles touch internally, distance between their centers = (R – r) cm
According to the given condition –
Or, R – r = 6 ......................(i)
Sum of their areas = (πR² + πr²) cm²
So, as per the given condition –
(πR² + πr²) = 116π
Or, π (R² + r²) = 116 π
Or, (R² + r²) = 116 ......................(ii)
We have the identity, (R + r)² + (R – r)² = 2(R² + r²)
Or, (R + r)² + 6² = (2 X 116)
Or, (R + r)² = 232 – 36 = 196
Or, (R + r)² = 14²
Or, (R + r) = 14 ...................(iii)
Now we will add (i) & (iii), and we get –
R + r = 14
R – r = 6
---------------
2 R = 20
Or, R = 10
Now we will substitute the value of R in (iii), and we get -
R + r = 14
Or, 10 + r = 14
Or, r = 14 – 10 = 4
Now, the radii of the circles are 10 cm & 4 cm respectively. (Ans.)