CLASS-9
AREA OF AN EQUILATERAL TRIANGLE
Area of an Equilateral Triangle –
Let ABC be an equilateral triangle with side a and AD be the perpendicular from A on BC. Then D is the mid-point of BC i.e. BD = a/2
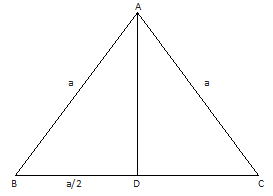
The right angled △ ABD, by Pythagoras theorem, we have –
AD² = AB² - BD²
As per the above condition, AB = a, and BD = a/2
So, AD² = AB² - BD²
a a²
AD² = a² - (-----)² = a² - ------
2 4
4a² - a² 3a²
AD² = ------------ = --------
4 4
3a² √3a
AD² = ------- = (--------)²
2² 2
√3a
AD = -------
2
1
So, the area of △ ABC = ------- X BC X AD
2
1 √3a
= ------- X a X --------
2 2
√3a²
= -------
4
So, Area of Equilateral Triangle with side a units = √3/4 a² sq. units
Height of the Equilateral Triangle is = √3a/2 units
Example.1) Calculate the area of an equilateral triangle of side 20 cm, correct to two decimal places. Also find its height correct to one decimal places (take √3 = 1.732).
√3
Ans.) Area of the triangle = (------- X a²) sq. units
4
√3
= (------- X 20 X 20) cm²
4
= (√3 X 100) cm²
= (1.732 X 100) cm² = 173.20 cm²
√3
Height of the triangle = (------ X a) cm
2
√3 √3
So, ------ X a = (------- X 20)
2 2
= (√3 X 10) cm = (1.732 X 10) cm
= 17.32 cm = 17.3 cm (Ans.)
Example.2) Calculate the area of an equilateral triangle whose height is 14 cm. (take √3 = 1.73)
Ans.) Let the side of the triangle be a cm.
√3
Then its height => (------ X a) cm = 14
2
28
So, a = ------- cm ………………….(i)
√3
√3
Area of the triangle = (------- X a²) cm²
4
√3 28 28 7 X 28
= ------- X ------- X -------- = -----------
4 √3 √3 √3
7 X 28
= ---------- = 113.29 cm²
1.73
Hence the area of the equilateral triangle is 113.29 cm² (Ans.)