CLASS-9
ARE OF ISOSCELES TRIANGLE

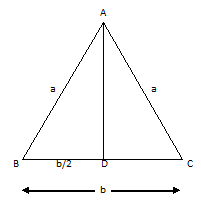
Then, D is the mid-point of BC, i.e. BD = b/2

In right angled △ ABD, by Pythagoras theorem, we have – 

                       AD² = AB² - BD²

                                         b

              =>       AD² = a² - (------)²

                                         2

                                         b²         4a² - b²

              =>       AD² = a² - ------- = ------------

                                         4              4

                                    √(4a² - b²)

              =>        AD  =  --------------

                                         2

                                1

So, the area of △ABD = ------- X BC X AD

                                2

                               1              √(4a² - b²)

                          = ------ X b X -------------

                               2                    2

                                 1

                          =  ------- b √(4a² - b²)

                                 4

So, area of Isosceles △ABC with AB = AC = a units and BC = b units

                                  1

                        =   --------- b √(4a² - b²) sq units

                                  4

Perimeter of isosceles triangle = (2a + b) units

Example.) The perimeter of an isosceles triangle is 42 cm and base is

         1

1 ------- times each of the equal

      2

sides. Find -  i) the length of each side of the triangle

                ii) the area of the triangle

                iii) the height of the triangle

Ans.)  i) let each of the equal side of the triangle is a cm & base b cm

                        1             3a

     Then,  b =  1 ------ a = --------

                        2              2 

            So,   a + a + b =  42

                  3a

So,  a + a + -------- =  42

                   2

       2a + 2a + 3a

So, --------------- =  42

             2

         7a

So, ---------  =  42

          2

              42 X 2

So,  a  = ----------- =  12 cm

                 7                                                                                              

So, each equal side => a = 12 cm,

                                   3

and base =>  b = ------ X 10 = 18 cm        (Ans.)

                       2

                                 1

ii) Area of the triangle =  (------ b√4a² - b²) cm²

                                 4

                               1

                          = ------ X 18 X (√4 X 12² - 18²)

                               4

                               18

                          = ------- √576 – 324   

                                4

                             9

                       = ------- X 15.87 = 71.41 cm²   (Ans.)

                             2

                                    √4a² - b²

iii)  Height of the triangle =  (------------)

                                         2

                                  √(4 X 12²) - 18²

                             = ------------------

                                          2

                          √576 – 324         15.87

                     = ------------- = ---------- = 7.94 cm   (Ans.)

                               2                 2

Example.2) The base of an isosceles triangle is 24 cm and its area is 192 cm² find its perimeter.

Ans.)   Given b = 24 cm

As per the formulae –

                              1

                Area =  (------- b√4a² - b²) cm²

                              4

                                    1

             =>   192 cm² =  (------ 24 √4a² - 24²)

                                    4

                =>     6√4a² - 24²  =  192

                =>     6√(4a²- 576) =  192

                =>     6√4 (a² - 144) = 192

                =>     (6 X 2) √a² - 144 = 192

                =>       √a² - 144 = 16

                =>       (√a² - 144)² = 16²

                =>       a² - 144 = 256

                =>       a² = 256 + 144 = 400

                =>        a² = 20²

                =>         a = 20

So, side of the isosceles triangle a = 20, and base b = 24

Hence, the required perimeter = (2a + b) = {(2 X 20) + 24}

                                              = 40 + 24 = 64 cm          

Hence the perimeter of the said isosceles triangle is 64 cm    (Ans.)