CLASS-8
WORD PROBLEM OF VENN DIAGRAM
WORD PROBLEM
Example.- A) Out of 50 students in a class someone like either Chocolate or Cake or both, 25 like Chocolate while 15 like both. Draw a Venn diagram and find the number of students who like 1) Cake, 2) Only Cake and 3) Only Chocolate.
Answer) Let decide C = { students who likes Chocolate }, M = { students who like Cake }
Then n(C) = 25
n (C U M) = number of students who like either chocolate or milk or both = 50 and n(C ∩ M) = number of students who like both = 15
Now, as per the rules n (C U M) = n(M) + n(C) - n(C ∩ M)
Or, 50 = n(M) + 25 – 15
Or n(M) = 40
Number of students who like Cake n(M) = 40
Number of students who like both Chocolate and Cake n(C ∩ M) = 15
The number of students who like only Chocolate = n(M) - n(C ∩ M)
= 40 – 15
= 25
And the number of students who like Cake = n(C) - n(C ∩ M)
= 25 – 15
= 10
If we show this obtained figure in the Venn diagram, then it looks like -
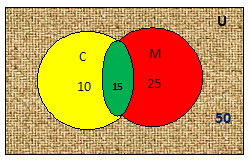
In this diagram -
Total students of class = 50
Number of Students who like Chocolate = 25
Number of students who like Cake = 10
Number of students who like both Chocolate & Cake = 15
Example.-B) Out of a class of 120 students, 80 students likes a have math, 70 students like Physics and all like either math or physics or both, find the number of students who like 1) both math physics & math, 2) only math, 3) only physics
Answer) Let us assume –
M = { students who like Math }, P = { students who like Physics }
M U P = { students who like either math or physics }
M ∩ P = { student who like both }
As per the given condition, n(M) = 80, n(P) = 70, n(M U P) = 120
Let, n(M ∩ P) = the number of students who like both = B
Then the number of students who like only math = 80 – B
And the number of students who like only physics = 70 – B
So, the total number of students = 120 = (80 – B) + B + (70 – B)
Or, 120 = 150 – B
Or, B = 150 – 120 = 30
1) so, the number of students who like both math & physics = B = 30
2) the number of students who like only math = 80 – B
= 80 – 30 = 50
3) the number of students who like only physics = 70 – B = 40
If we show this obtained figure in the Venn diagram, then it looks like -
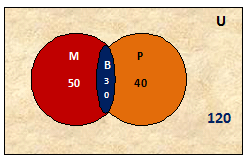
In this diagram –
Total number of students = 120
Number of students who like Math = 50
Number of Students who like physics = 40
Number of students who like both = 30
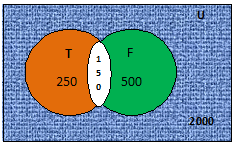
Example.-C) Out of a group of 2000 people, 250 like to watch Tennis, 500 like to watch football and 150 watch both, find the number of people who like to watch – 1) only tennis, 2) only football, 3) either tennis or football or both, 4) neither tennis nor football
Answer) let us assume –
Let, U = { the entire group }, T = { People who like to watch tennis },
F = { people who like to watch football }
As per the given condition, n(T) = 250, n(F) = 500, n(T ∩ F) = 150
1) the number of people who watch only Tennis =
n(T) – n(T ∩ F) = 250 – 150 = 100
2) the number of people who watch only football =
n(F) – n(T ∩ F)
= 500 – 150 = 350
3) the number of people who watch either tennis or football or both =
n (T U F) = n(T) + n(F) - n(T ∩ F)
= 250 + 500 – 150 = 600
4) the number of people who watch neither tennis nor football
n(U) - n (T U F) = 2000 – 600 = 1400