CLASS-8
RELATION & MAPPING - FUNCTION & RELATION

Function & Relation -

We have already discussed earlier about the relation & mapping but now we would like to discussed about the function & relation. There are some example are given below

This is to be remembered that –

1) All functions are relations but all relations are not functions.

The domain of relation (1) = {1, 2, 3, 4, 5} = set A and the domain of relation (5) = {1, 2, 3, 4, 5} = set A

2) The domain of a mapping or function from set A to set B = set A

The range of relation (1) = {a, b, c, d, e} = set B, while the range of relation (5) = {a, b, c, d, e} ⊂ set B

Next, consider the relation “is half of” from set A = {3, 5, 7, 9} to set B = {6, 10, 14, 18}, illustrated by the arrow diagram alongside.

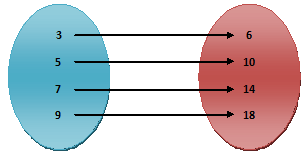
It is clear that, 2 R 4,  5 R 10,  7 R 14,  9 R 18, the relation is a function because each element of A is associated with only one member of B. If we denote this relation by ‘f ’ then we can represent the function ‘f’ from set A to set B as f : A → B.

We can write f(3) = 6, similarly  f(5) = 10,  f(7) = 14, and f(9) = 18. In other words the images of  3, 5, 7 & 9 are 6, 10, 14, & 18 respectively. We can represent f in the roster form as –

 f = {(3, 6), (5, 10), (7, 14), (9, 81)} where 3, 5, 7, 9 belongs to set A and 6, 10, 14, 18 belongs to set B

or, f = {(x, y) : x Є A, y Є B and y = 2x}

if ‘x’ is an element of A then the image of ‘x’ is 2x, i.e., f(x) = 2x

so, f = {(x, f(x)) such that x Є A} = {(x, f(x) : x Є A}

we can also write, f : A → B such that f(x) = 2x, x Є A       

this is the equation form of the functions, The set A is called the domain of the function ‘f ’, the set B is called the co-domain of the function ‘f’ and the set of all the images of the elements of A is called the range of the function ‘f’.

Next, consider the relation “is double of” from set A = {49, 64, 81, 121} to set B = {7, 8, 9, 11}, illustrated by the arrow diagram alongside.

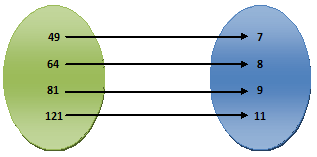
It is clear that, 49 R 7,  64 R 8,  81 R 9,  121 R 11, the relation is a function because each element of A is associated with only one member of B. If we denote this relation by ‘f ’ then we can represent the function ‘f’ from set A to set B as f : A → B.

We can write f(49) = 7, similarly  f(64) = 8,  f(81) = 9, and f(121) = 11. In other words the images of  49, 64, 81 & 121 are 7, 8, 9, & 11 respectively. We can represent f in the roster form as –

   f = {(49, 7), (64, 8), (81, 9), (121, 11)} where 49, 64, 81, 121 belongs to set A and 7, 8, 9, 11 belongs to set B

or, f = {(x, y) : x Є A, y Є B and 2x = y}

if ‘x’ is an element of A then the image of ‘x’ is 2x, i.e., f(2x) = x

so, f = {(x, f(2x)) such that x Є A} = {(x, f(2x) : 2x Є A}

we can also write, f : A → B such that f(2x) = x, 2x Є A       

this is the equation form of the functions, The set A is called the domain of the function ‘f ’, the set B is called the co-domain of the function ‘f’ and the set of all the images of the elements of A is called the range of the function ‘f’.