CLASS-8
CONDITION FOR RELATION TO BE A FRACTION
Condition for a relation to be a function –
1) When the relation is expressed in the roster from – every element of A must appear as first element of an ordered pair. Also, the first element of the ordered pairs must be different.
In other words, two or more ordered pairs of the relation must not have the same first element. However, the second element of the ordered pairs may be repeated.
2) when the relation is represented by an arrow diagram – every element of A must have one and only one image in B. However, two or more elements of A may have the same image in B
There are some example are given below -
Example.1) Determine whether the given relation can be a function.
a) R = {(5, 8), (6, 8), (7, 8)},
the first elements of the ordered pairs of R are different. So, this relation can be a function
b) R = {(7, 2), (0, 0), (7, -2)}
this relation cannot be a function because the number ‘7’ is the first elements in more than one ordered pair.
Example.2) Does the arrow diagram represent a function? If, so express the function in the roster form and in the equation form. Also, find the domain and range of the function
Ans.) The relation is a function from set A to set B,
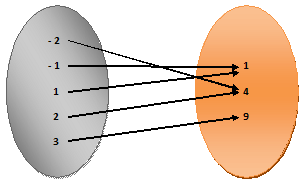
because each element of A has a unique image in B the function f in the roster form is
So, f = {(-2, 4), (-1, 1), (1, 1), (2, 4), (3, 9)}
Since, f (-2) = 4 = (-2)²,
f(-1) = 1 = (-1)²,
f(1) = 1 = 1²,
f(2) = 4 = 2²
and, f(3) = 9 = 3², we have f(x) = x², x Є A,
so, the equation form of function f is –
f(x) = x² or f : x → x², x Є A
the domain of f = {-2, -1, 1, 2, 3} and the range of f = {1, 4, 9}
Example.3) Let A = {2, 4, 7}, B = {4, 16, 49, 81} and f : A → B where f(x) = x², x Є A.
a) Draw an arrow diagram for this mapping
b) Represent f in the roster form
c) Find the domain and range of ‘f’
Ans.) here (x) = x², so f(2) = 2² = 4
f(4) = 4² = 16
f(7) = 7² = 49
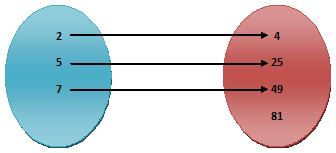
a) the arrow diagram is shown upside
b) the ordered pairs of f = (2, 4), (5, 25), (7, 49)
so, in the roster form f = {(2, 4), (5, 25), (7, 49)}
c) The domain of f = {2, 5, 7}
the range of f = {4, 25, 49}
Example.4) Let A = {1, 3, 5, 7}, B = {2, 3, 5, 8} and R be the relation “is less than or equal to” from A to B.
a) Write R in the roster form
b) Represent by an arrow diagram
c) find the domain and the range of R
d) is R a mapping ? give reasons.
Answer) 1 < 2, 1 < 3, 1 < 5, 1 < 8, 3 = 3, 3 < 5, 3 < 8, 5 = 5, 5 < 8, 7 < 8
So, the (1, 2), (1, 3), (1, 5), (1, 8), (3, 3), (3, 5), (3, 8), (5, 5), (5, 8), (7, 8)
a) the relation in the roster form is R = {(1, 2), (1, 3), (1, 5), (1, 8), (3, 3), (3, 5), (3, 8), (5, 5), (5, 8), (7, 8)}
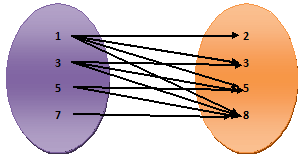
b) the adjoining arrow diagram represents R
c) the domain of R = {1, 3, 5, 7}, the range of R = {2, 3, 5, 8}
d) this relation is not a mapping because the members 3 and 5 of the set A are matched with more than one member of the set B.
Example.5) Draw an arrow diagram for the relation R = {(-1, -3), (0, 0), (1, 3), (2, 6)}, is this relation a function? If so, express it in the form of an equation, also find the domain and the range of function.
Ans.) The arrow diagram has shown alongside –
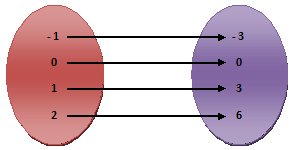
The relation is a function from set A to set B, because each element of A has a unique image in B. Since the image of each element of A is thrice the element, the function can be expressed as
So, f(x) = 3x, x Є A or f : x → 3x, x Є A
The domain of f = {-1, 0, 1, 2} and the range of f = {-3, 0, 3, 6}
Example.6) Let, f : x → 3x + 2, where A = {1, 2, 3, 4} and B is the set of images of the elements of A.
a) Find B & f
b) Draw an arrow diagram
c) Fin the domain and range of f
Answer) Here, f(x) = 3x + 2 …………………….(1)
So now, A = {1, 2, 3, 4}, substituting x = 1, 2, 3, 4 respectively in (1), we get
f(1) = 3x + 2 = 3.1 + 2 = 5
f(2) = 3x + 2 = 3.2 + 2 = 8
f(3) = 3x + 2 = 3.3 + 2 = 11
f(4) = 3x + 2 = 3.4 + 2 = 14
so, the images of the elements 1, 2, 3, & 4 of A are 5, 8, 11, & 14 respectively.
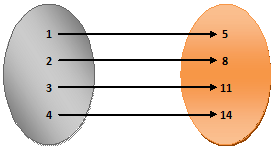
a) B = set of images of elements of A = {5, 8, 11, 14}
so, f = {(1, 5), (2, 8), (3, 11), (4, 14)}
b) the arrow diagram is shown above
c) the domain of f = {1, 2, 3, 4} and the range is f = {5, 8, 11, 14}