CLASS-8
RELATION & MAPPING - ARROW DIAGRAM (SOME OTHER WAY)

Similarly, on the other Way -

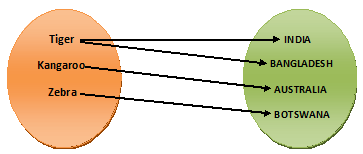
The animals (the elements of the first set) and the countries (the elements of the second set) are linked by a relation “ is the national animal of ”. The arrows are drawn between the ordered pairs, or matching pairs, of elements that satisfy the relations.

A relation is a link between the elements of two sets based on some common property. We know the two ways of representing relations – by making arrow diagrams and by expressing in the roster form.

Roster Form –

Let us call the set of animals A and the set of countries B, to express the relations between the two sets in the roster form, we write the matching, or ordered pairs (Tiger, India), (Tiger, Bangladesh), (Kangaroo, Australia), (Zebra, Botswana). Then the pair (Tiger, India) means “Tiger is the national animal of India”. Thus we get –

A = {Tiger, Kangaroo, Zebra}, B = {India, Bangladesh, Australia, Botswana} and R = {(Tiger, India), (Tiger, Bangladesh), (Kangaroo, Australia), (Zebra, Botswana)}.

Where R is the relation from the set A to the set B.

Please notice that, while writing the ordered pairs we have written the elements of the set A first. This is because the relation is from the set A to the set B.

To express a relation  from set A to set B in the roster form , we should write the elements of set A first and to express a relation from set B to set A, we should write the elements of set B first.

We could also write Tiger R India, Tiger R Bangladesh, Kangaroo R Australia,  Zebra R Botswana, here R stands for “is the national animal of”.

Thus,  R = {(a,b) : a Є A, b Є B and a is the national animal of b}