CLASS-8
PROBLEM & SOLUTION OF CONGRUENT
PROBLEM & SOLUTION OF CONGRUENT
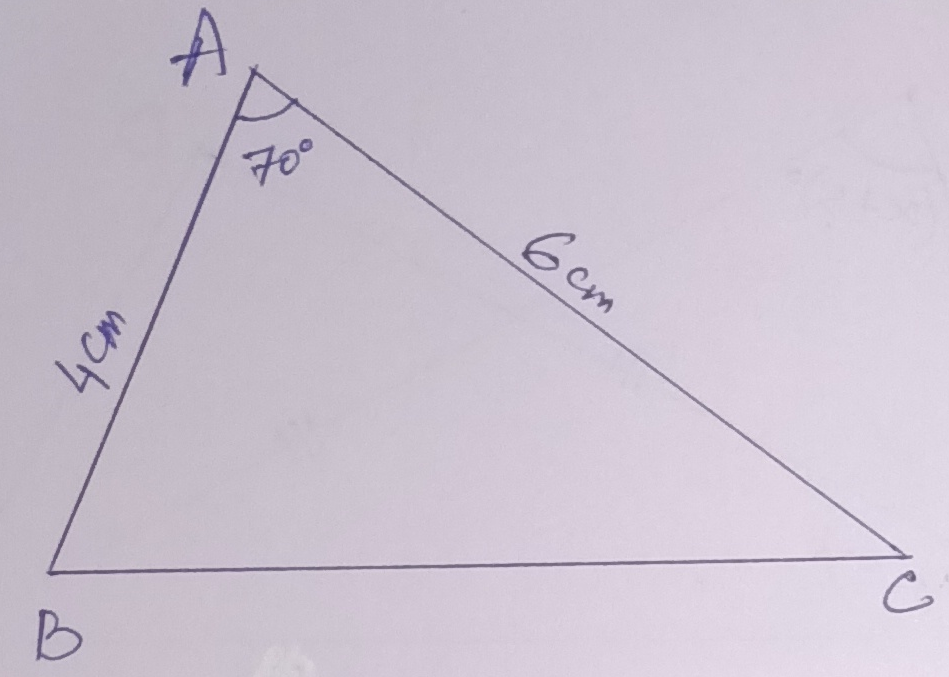
Example.1) State whether the triangles in the figure are congruent.
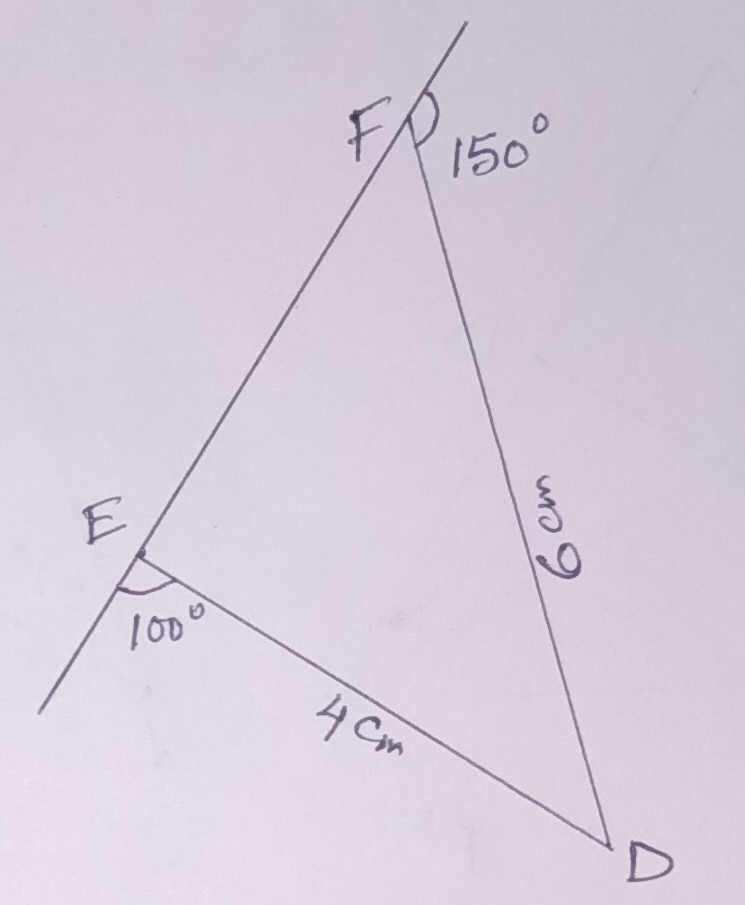
Ans.) In ∆ DEF,
∠DEF = 180⁰ - 100⁰ = 80⁰
∠EFD = 180⁰ - 150⁰ = 30⁰
So, ∠EDF = 180⁰ - (80⁰ + 30⁰) = 70⁰
In, ∆ ABC & ∆ DEF, AB = DE, ∠BAC = ∠EDF (= 70⁰) and AC = DF.
So, the S-A-S condition of congruence is satisfied.
So, ∆ ABC ≅ ∆ DEF
Example.2) In the adjoining figure, ∠ABD = ∠ACD & AD ⊥ BC, prove that –
1) ∆ ABD ≅ ∆ ACD
2) D is the mid-point of BC and
3) ∠BAD = ∠CAD, that is, AD bisects ∠BAC
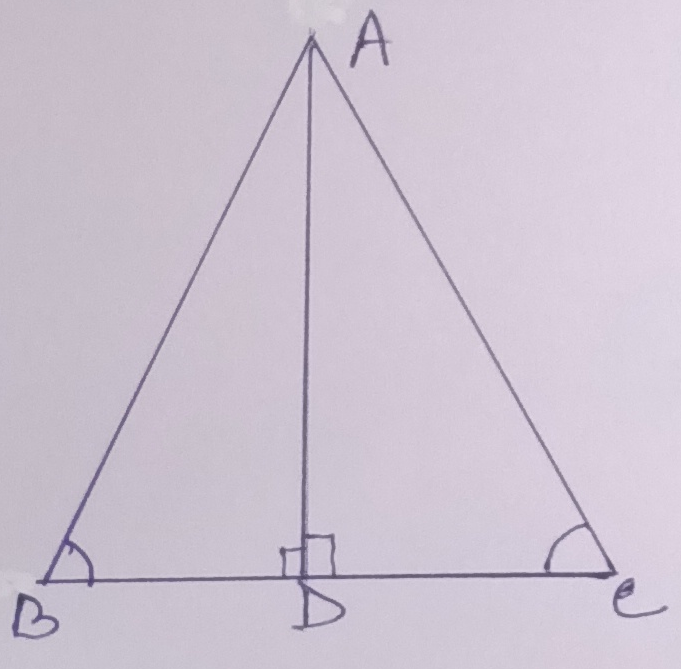
Ans.)
1) given, ∠ABD = ∠ACD => AC = AB
In ∆ ABD and ∆ ACD, ∠ABD = ∠ACD, ∠ADB = ∠ADC (= 90⁰) and AB = AC .
So, A-A-S condition of congruence is satisfied.
∆ ABD ≅ ∆ ACD
2) the corresponding parts of ∆ ABD and ∆ ACD are equal
So, BD = CD, that is, D is the mid-point of BC
3) also, ∠BAD = ∠CAD, that is, AD bisects ∠BAC
Example.3) In the adjoining figure, AB bisects ∠CAD and AC = AD, prove that (a) ∆ ABC ≅ ∆ ABD and (b) BC = BD
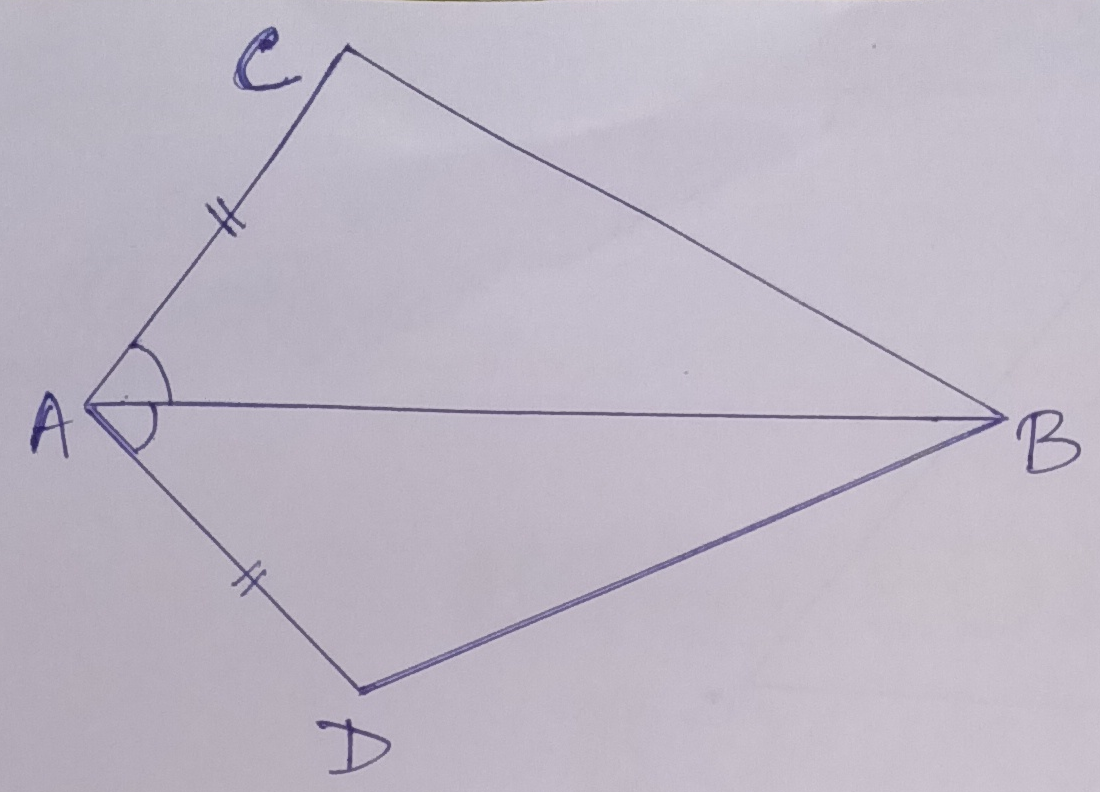
Ans.) ∆ ABC and ∆ ABD,
AC = AD (given),
∠BAC = ∠BAD (where AB bisects ∠CAD )
AB = AB
So, the S-A-S condition is satisfied.
So, ∆ ABC ≅ ∆ ABD
(b) the corresponding sides of ∆ ABC and ∆ ABD are equal.
So , BC = BD
Example.4) In the adjoining figure, prove that – (a) ∆ DBC ≅ ∆ EAC and (b) DC = EC
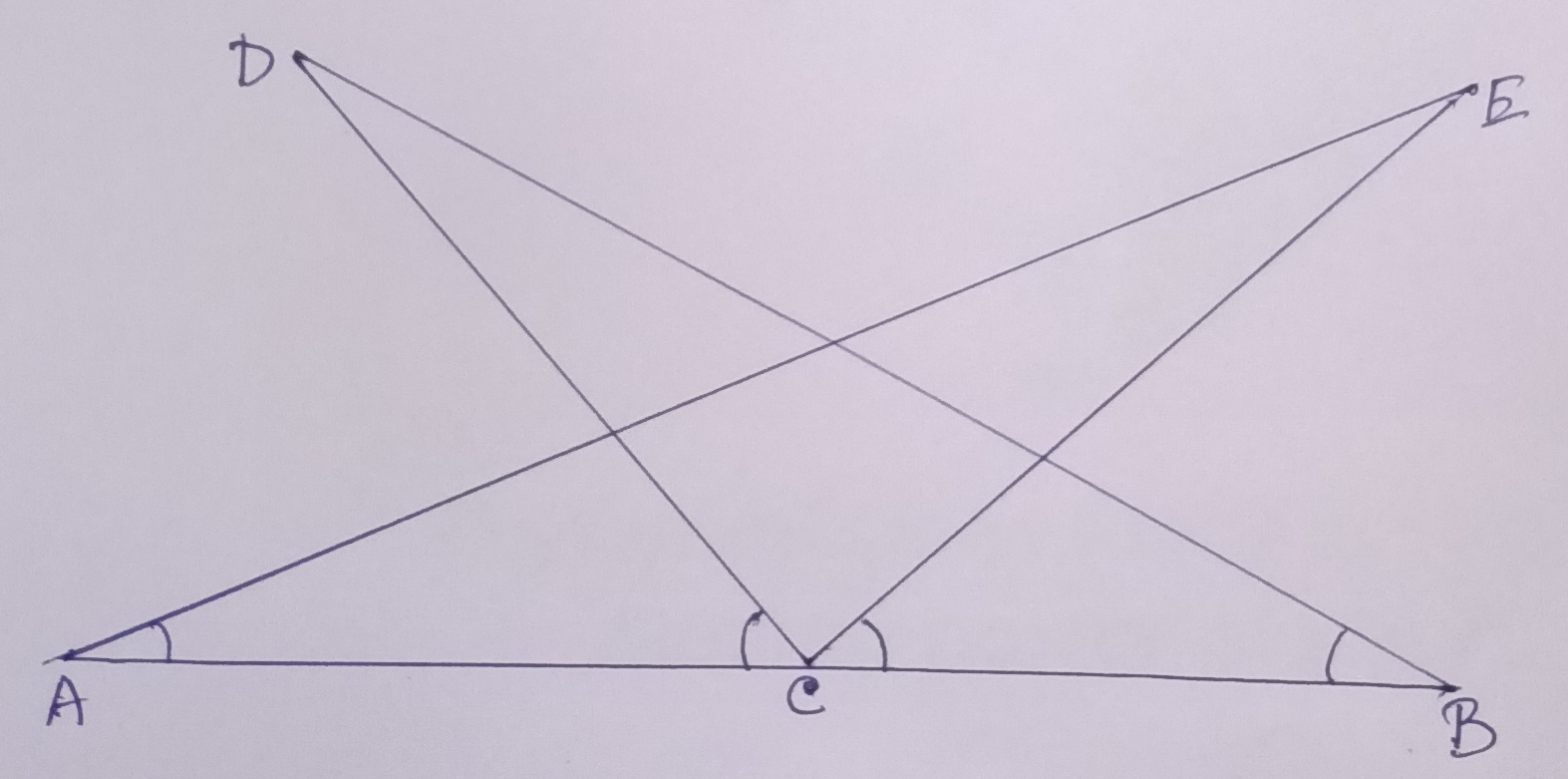
Ans.) As per the given condition, ∠ECB = ∠DCA
Adding, ∠DCE to both sides,
∠ECB + ∠DCE = ∠DCA + ∠DCE
=> ∠DCB = ∠ECA ………………………. (a)
In ∆ DBC and ∆ EAC, ∠DCB = ∠ECA [using (a)], BC = AC (given)
And, ∠DBC = ∠EAC (given)
So, the A-S-A condition is satisfied,
So, ∆ DBC ≅ ∆ EAC.
The corresponding sides of ∆ DBC and ∆ EAC are equal.
So, DC = EC …………………………………….(b)
Example.5) In the adjoining figure, AB = CD and AB || CD. Prove that –
a) ∆ AOB ≅ ∆ DOC and
b) AD & BC bisect each other at the point ‘0’
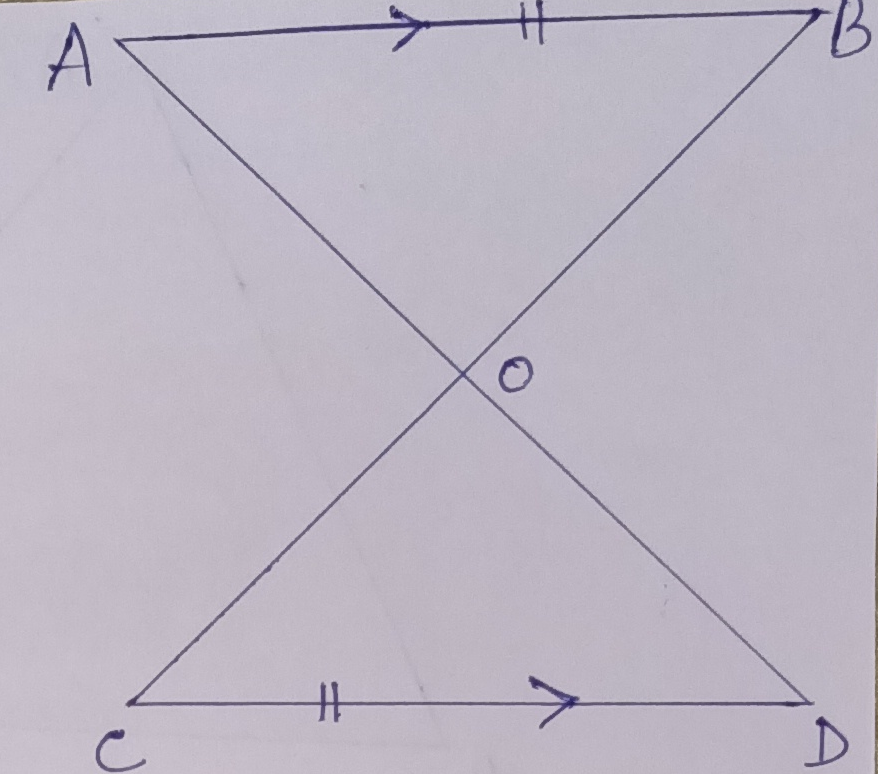
Ans.) AB || CD => ∠OAB = alternate ∠ODC and ∠OBA = alternate ∠OCD
a) In ∆ AOB and ∆ DOC,
∠OAB = ∠ODC,
∠OBA = ∠OCD and AB = CD
so, the A-S-A condition of congruence is satisfied.
So, ∆ AOB ≅ ∆ DOC
b) so, the corresponding sides of ∆ AOB and ∆ DOC are equal.
So, AO = DO and BO = CO
Hence, AD & BC bisect each other at the point O
Example.6) In the adjoining figure figure, BD = CE and ∠ADB = 90⁰ = ∠AEC, prove that –
a) ∆ ABD ≅ ∆ ACE and
b) ABC is an isosceles triangle in which AB = AC
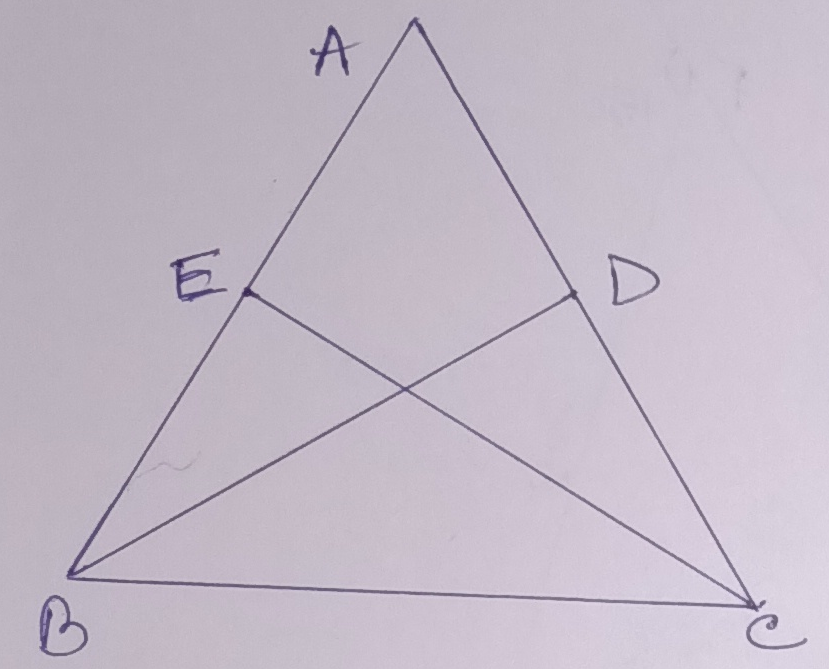
Ans.)
a) In ∆ ABD and ∆ ACE, ∠ADB = ∠AEC (=90⁰) (given)
∠BAD = ∠CAE and BD = CE (given)
The A-A-S condition of congruence is satisfied.
So, ∆ ABD ≅ ∆ ACE
b) The corresponding sides of ∆ ABD and ∆ ACE are equal.
So, AB = AC, that is, ABC is an isosceles triangles
Example.7) Find x & y in each of the following figure.
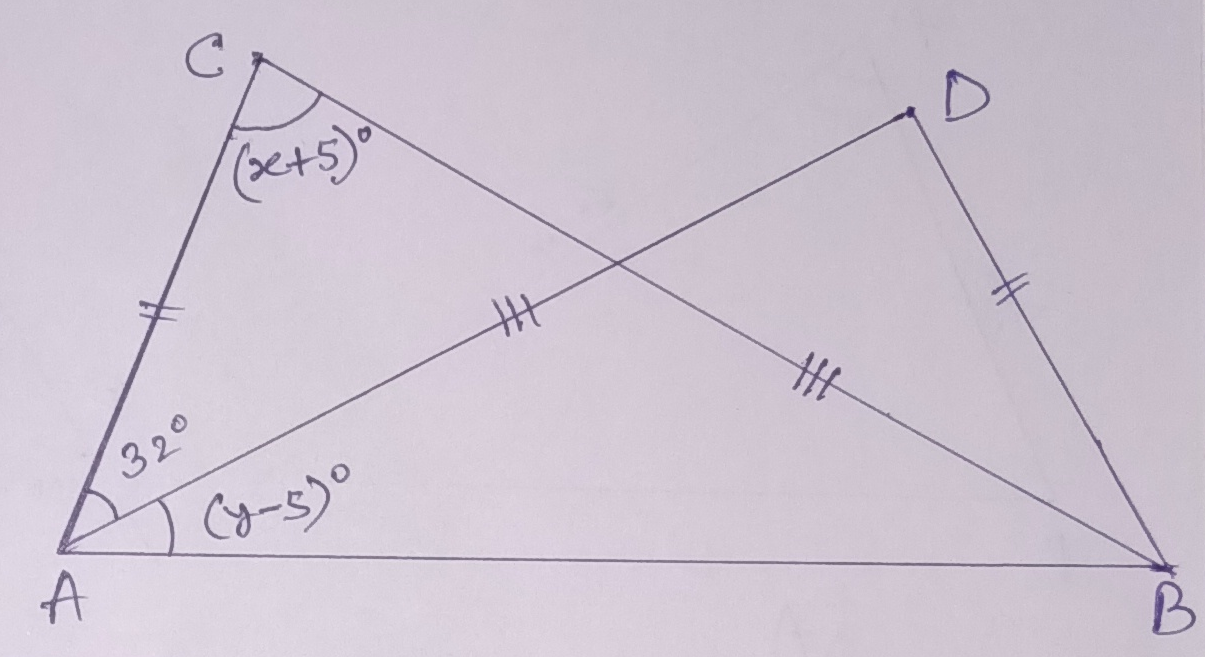
Ans.)
a) In ∆ CAB and ∆ DBA, AC = BD (given),
BC = AD (given)
And, AB = AB
So, ∆ CAB ≅ ∆ DBA (S-S-S condition)
So, ∠ACB = ∠BDA, ∠CBA = ∠DAB = (y – 5)⁰ and ∠CAB = ∠DBA,
x + 5 = 64 or, x = 59
in, ∆ ABC, (x + 5)⁰ + 32⁰ + (y – 5)⁰ + (y – 5)⁰ = 180⁰
now, 59 + 5 + 32 + 2y – 10 = 180
or, 2y = 180 – 86 = 94
or, y = 94 / 2 = 47
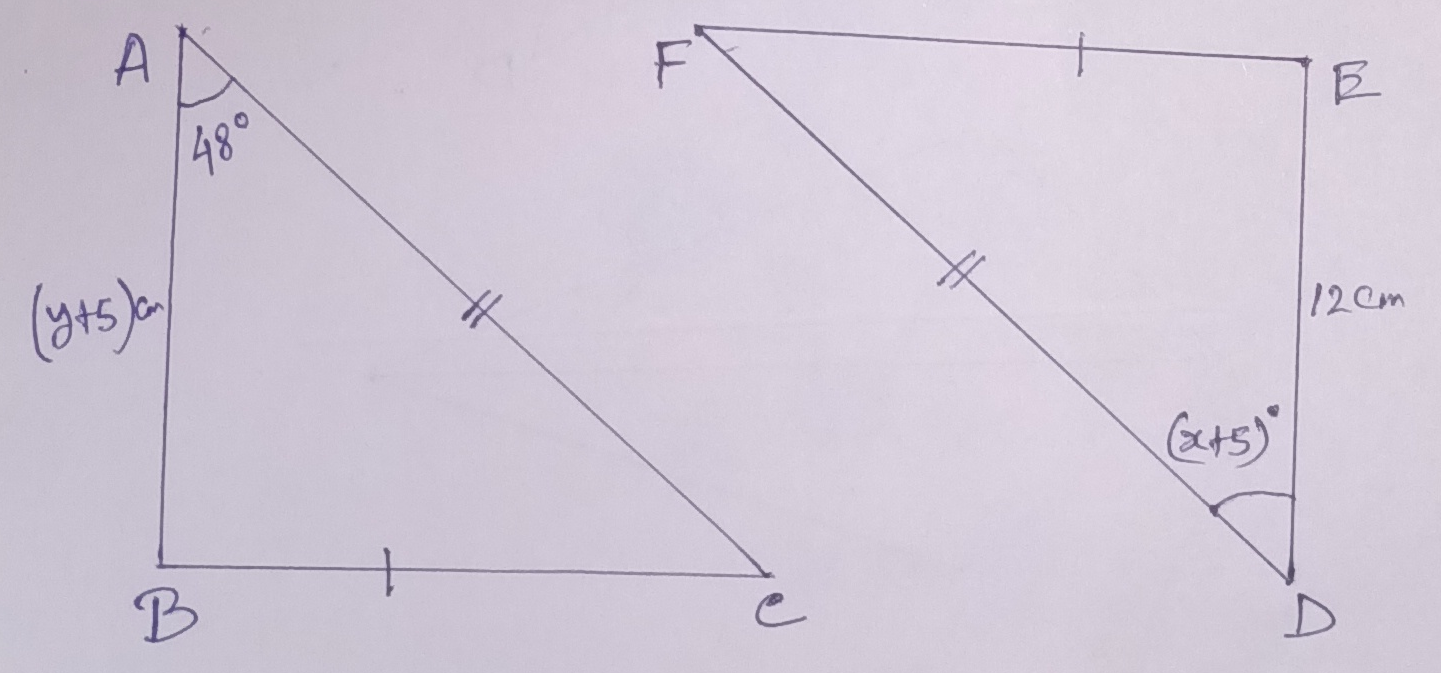
b) In, ∆ ABC and ∆ DEF, ∠ABC = ∠DEF = 90⁰, hypotenuse AC = hypotenuse DF (given) and BC = EF (given)
so, ∆ ABC ≅ ∆ DEF (R-H-S Condition)
or, 48⁰ = x + 5⁰ and y + 5 = 12
or, x = 43⁰ and y = 7