CLASS-8
INTERPRETING A VENN DIAGRAM

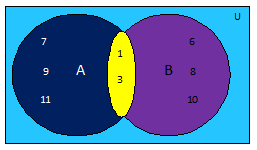
 So, universal set U  = { 1, 3, 6, 7, 8,  9, 10, 11 } and n(U) = 8

The closed region in the rectangle representing the set A contains the elements  1, 3, 7, 9, 11 while that representing the set B contains 1, 3, 6, 8, 10.

  A = { 1, 3, 7, 9, 11 } and  n(A) = 5

  B = { 1, 3, 6, 8, 10 } and  n(B) = 5

A U B = { 1, 3, 7, 9, 11 } U { 1, 3, 6, 8, 10 } = { 1, 3, 6, 7, 8, 9, 10, 11 }  and  n(A U B) = 8

And  A ∩ B = { 1, 3, 7, 9, 11 } ∩ { 1, 3, 6, 8, 10 }

             = { 1, 3 } and n (A ∩ B) = 2

And,  A – B =  { 7, 9, 11 }  and  n (A – B) = 3

Now, B – A =  { 6, 8, 10 }  and  n ( B – A ) = 3

A’ = ( U – A ) = { 1, 3, 6, 7, 8,  9, 10, 11 } – { 1, 3, 7, 9, 11 }

                = { 6, 8, 10 } 

And  n (A’) = 3

B’ = ( U – B )

  = { 1, 3, 6, 7, 8,  9, 10, 11 } – { 1, 3, 6, 8, 10 } = { 7, 9, 11 }

And  n (B’) = 3

(A U B)’ =  U - (A U B) 

   = { 1, 3, 6, 7, 8,  9, 10, 11 } - { 1, 3, 6, 7, 8, 9, 10, 11 } =  φ

And  n (A U B)’ =  φ

(A ∩ B)’ =  U - (A ∩ B)

=  { 1, 3, 6, 7, 8,  9, 10, 11 } – { 1, 3 } = { 6, 7, 8, 9, 10, 11 } 

And, n (A ∩ B)’ = 6