CLASS-8
GEOMETRY-TRIANGLES
TRIANGLES
A closed plane figure bounded by three line segments is called a triangle. In the figure, ABC is a triangle bounded by three line segments AB, BC, and CA. These are called the sides of the triangle.
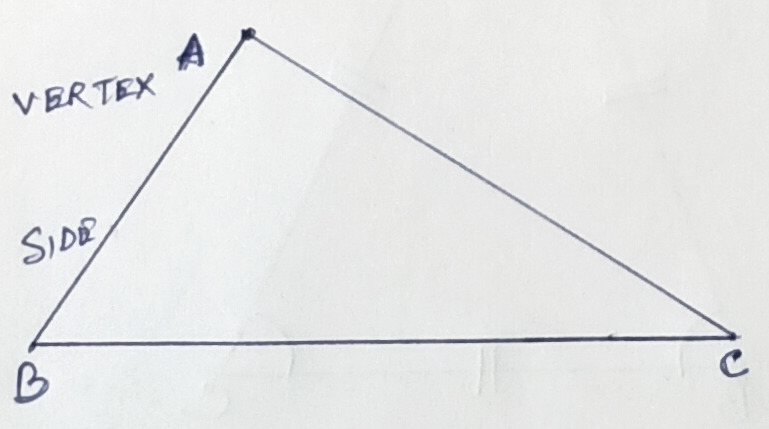
The points A, B, and C are called the vertices of the triangle. The angles ∠BAC, ∠ABC, and ∠BCA are called the interior angles or simply, the angles of the triangle. The three sides and the three angles of a triangle are together called the six parts (or elements) of the triangle.
Exterior Angles –
If the
side BC or ∆ ABC is produced to the
point ‘O’ then ∠ACO is called an exterior angle of ∆ ABC at ‘C’. ∠ACB and ∠ACO are adjacent
angles. So, ∠ACB + ∠ACO = 180⁰
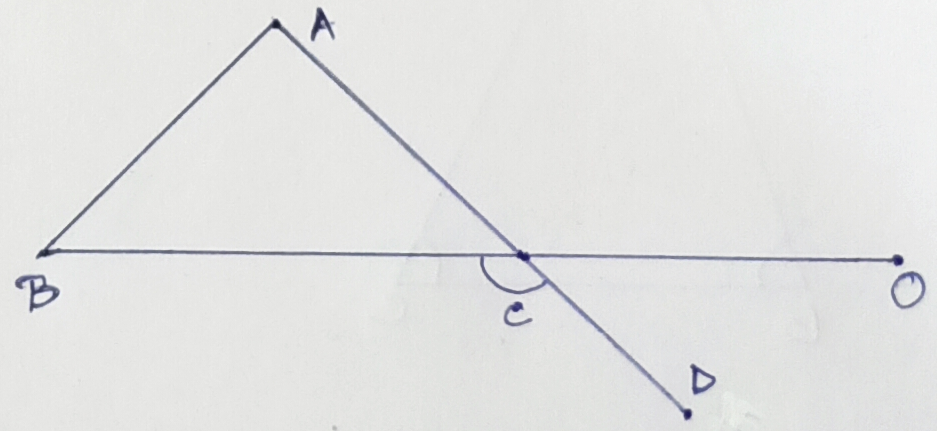
Exterior Angles + Adjacent Interior Angles = 180⁰
If AC is produced to D then ∠BCD will be another exterior angle of the ∆ ABC at C, being vertically opposite angles, ∠BCD = ∠ACO. Similarly there are two exterior angles of equal magnitude at each vertex.