CLASS-8
GEOMETRY-TRIANGLE-SOME-IMPORTANT-TERMS

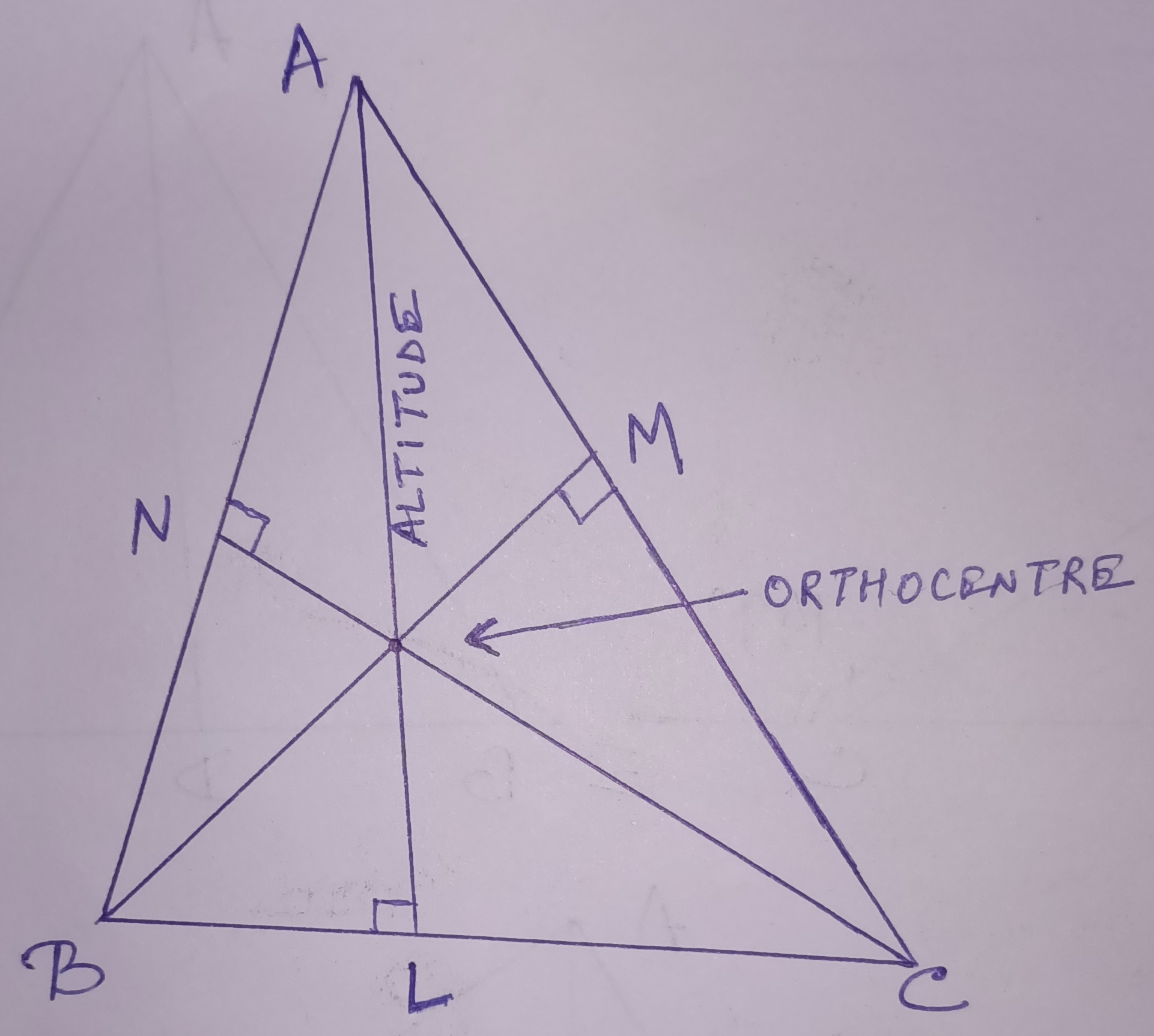
An altitude of a triangle is considered via drawing perpendicular from any vertex of the triangle to the opposite side. It is considered that, any triangle should have three altitudes. In the figure, AL, BM, and CN are the altitudes of said ∆ ABC.

The three altitudes of a triangle pass through a common point is considered or called the ‘orthocenter’ of any triangle.

Median -

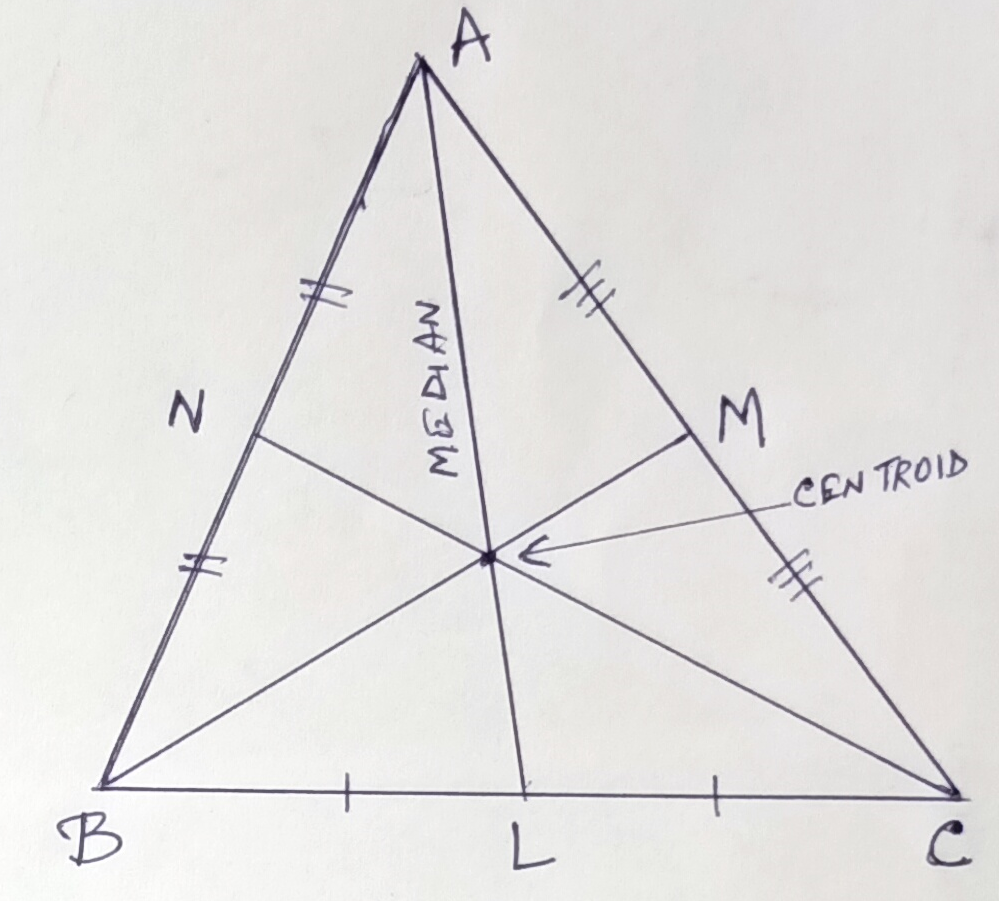
The line segment which is joining a vertex of a triangle to the midpoint of the opposite side is to be considered or called a median of the triangle. A triangle is considered to have three medians. In the figure, it has been seen that L, M, and N are the mid-points of the sides BC, CA, and AB respectively of the said triangle. So, AL, BM, and CN are considered as the medians of ∆ ABC.

The three medians of the said triangle intersect at the point is called or known as the ‘centroid’ or ‘centre of gravity of the said triangle’.

Incircle

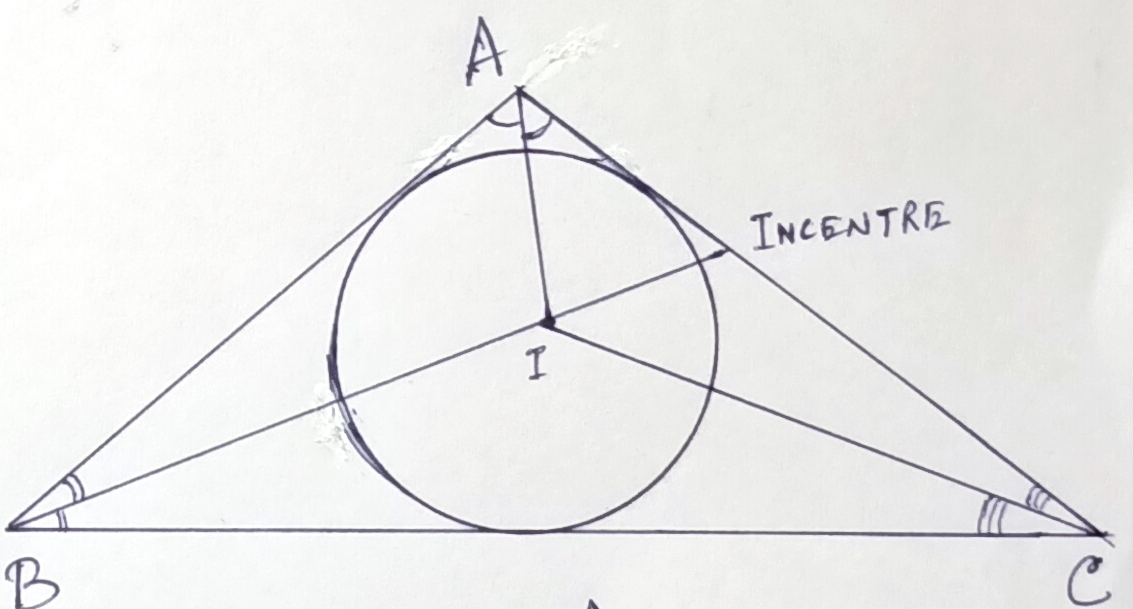
The circle that lies inside a triangle and touches its three sides then will be called or considered as the incircle. The centre of the incircle is called or to be considered as the incentre. The incentre is the point at which the three (internal) bisectors of the angles of the triangle is observed to meet each other. In the figure, we can observe that AI, BI, and CI bisect ∠A, ∠B, and ∠C respectively and meet at point I, which is to be considered incentre.

Circumcircle

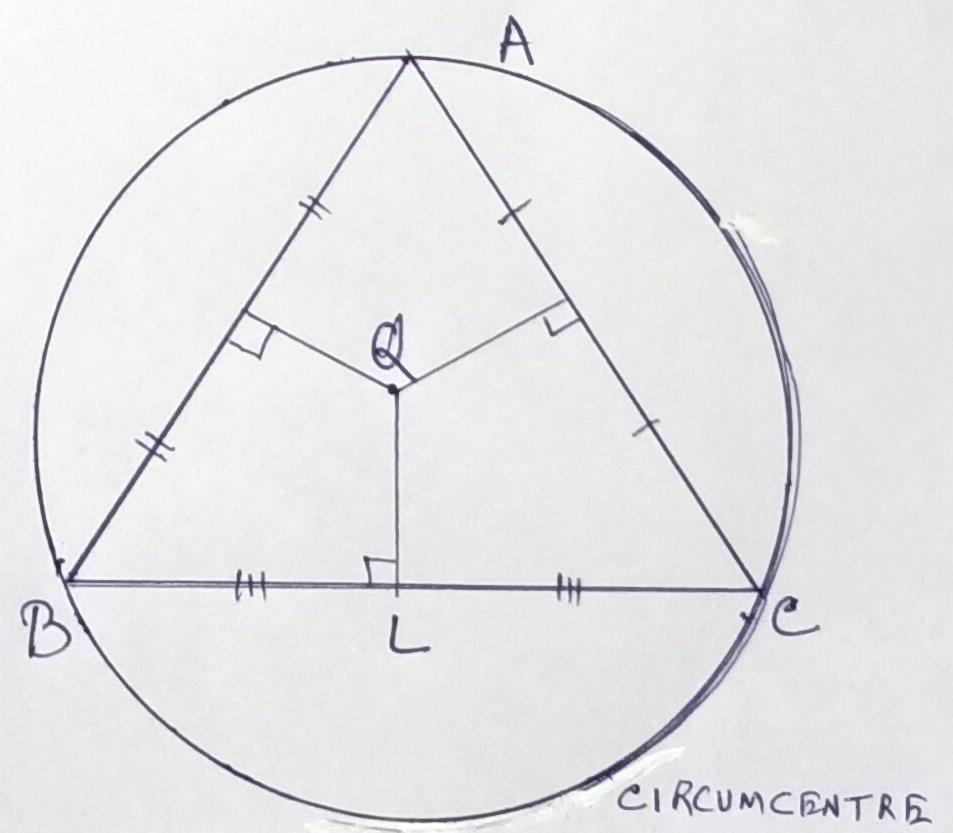
The circumcircle of a triangle is the circle which passes through its three vertices as we can observe from the given picture. Its centre is called the circumcentre, the point at which the perpendicular bisectors of the sides of the triangle when meets each other then this point is to be considered as circumcentre.