CLASS-8
GEOMETRY-TRIANGLE-CONGRUENCE OF TWO TRIANGLE 

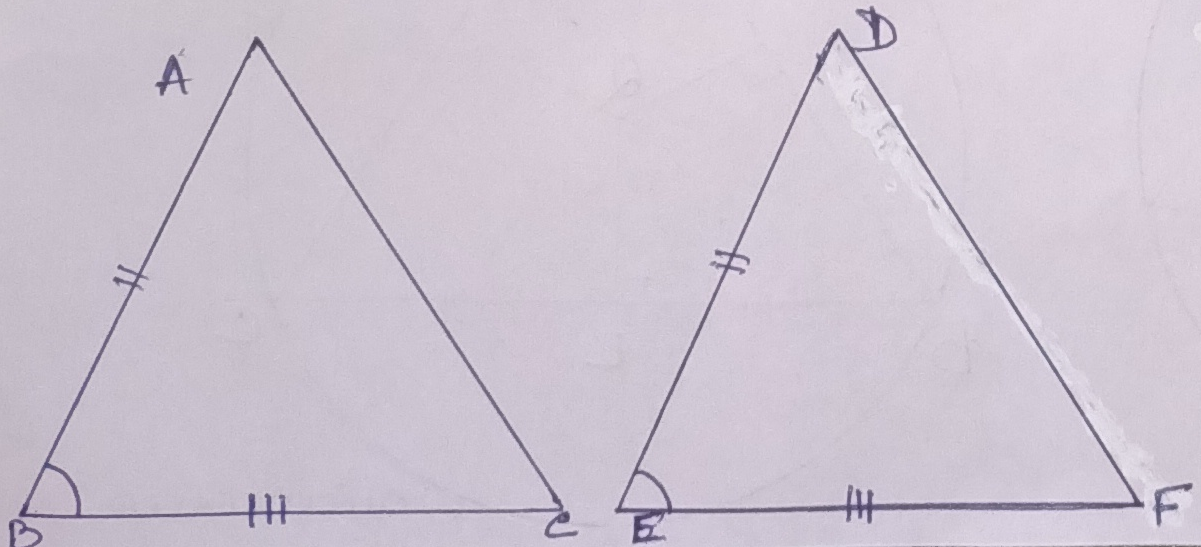
If any two sides and the included angle of one triangle are considered to be equal to the corresponding two sides of the triangle and the included angle of the other triangle then the two triangles are will be called congruent.

In,  ∆ ABC and ∆ DEF,

So, AB = DE, BC = EF, and ∠ABC =  ∠DEF,

 ∆ ABC ≅ ∆ DEF

Angle-Side-Angle (A-S-A) Condition -

If two angles and the included side of a triangle are considered to be equal to the corresponding two angles and the included side of the other triangle then the given two triangles are congruent.

In, ∆ ABC and ∆ DEF,  if ∠ABC = ∠DEF, ∠ACB = ∠DEF, and BC = EF, then ∆ ABC ≅ ∆ DEF

If two angles of ∆ ABC are equal to two angles of ∆ DEF then the third angles of ∆ ABC will be equal to the third angle of ∆ DEF because the sum of the three angles of any triangle is 180⁰. Thus we can say that two triangles are congruent if any two angles and one side of one triangle are equal to two angles and the corresponding side of the other triangle. This condition for congruence is denoted by Angle- Angle–Side (A-A-S)

Side-Side-Side (S-S-S) Condition –

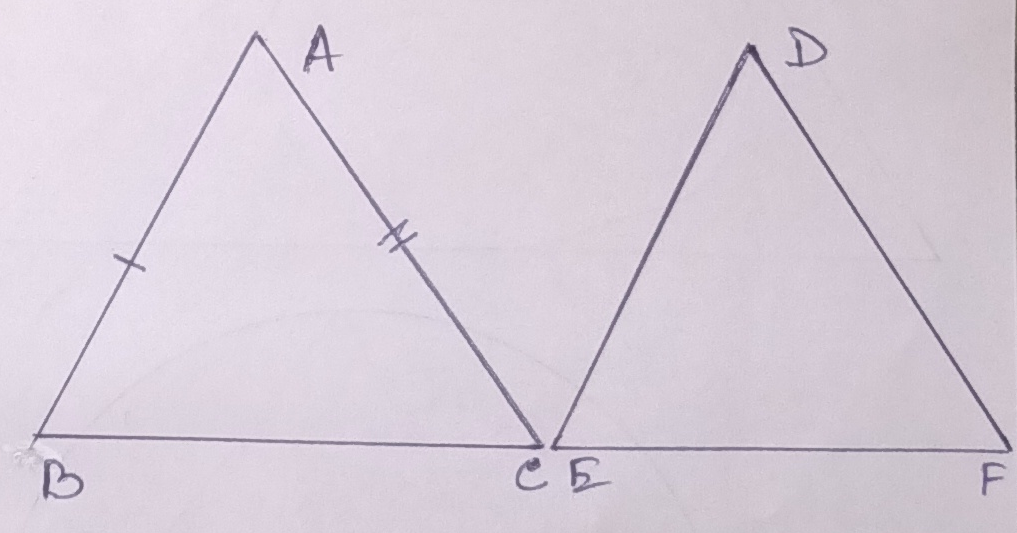
If three sides of one given triangle are equal to three sides of another given triangle then the obtained two triangles are considered to be congruent. In ∆ ABC and ∆ DEF, AB = DE, BC = EF and CA = FD.

So,   ∆ ABC ≅   ∆ DEF

Right Angle Hypotenuse-Side (R-H-S) Condition –

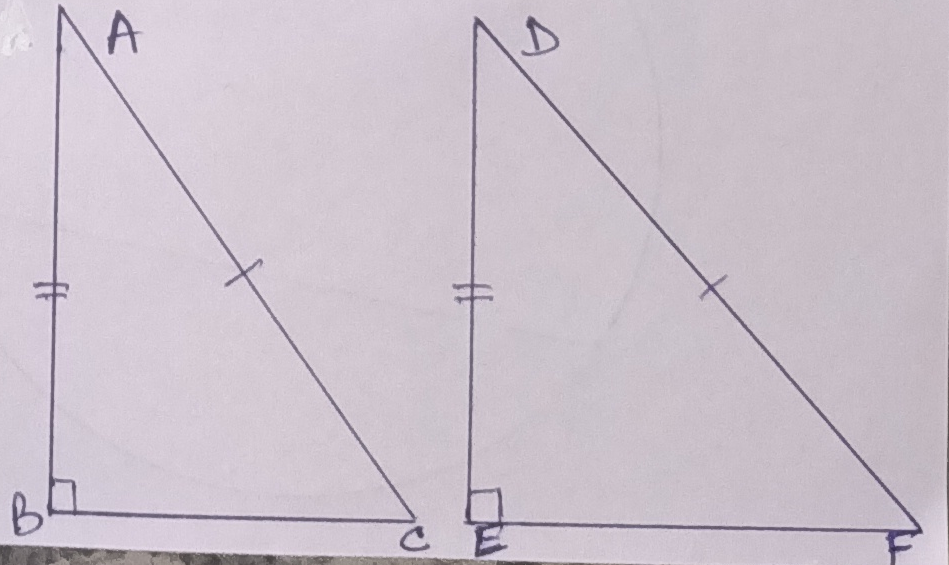
If the hypotenuse and one side of a right-angled of the given triangle are respectively equal to the hypotenuse and the corresponding side of the another right-angled of the given triangle then the two triangles are considered to be congruent.

In ∆ ABC and ∆ DEF, ∠ABC = ∠DEF = 90⁰,

Hypotenuse AC = hypotenuse DF and AB = DE,

So,  ∆ ABC ≅ ∆ DEF