CLASS-8
AREA OF TRIANGLE
AREA OF A TRIANGLE –
The term "Area" is already known by us, now we will learn the calculation of area of triangle, let us recall the definition of area.
Area – The area (A) of a closed plane curve is the region enclosed by the plane curve. The area of a plane figure is measured by square units such as square centimeter (cm²), square meter (m²)
Triangle – In this section he have to learn, how to calculate the area of a triangle.
1) Area of a Triangle –
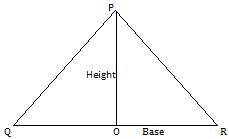
The area of a triangle will be considered by equal to half of the product of its base and the corresponding height (or altitude)
1
Area of a triangle = ------- X base X height
2
If, QR is considered as a base of ∆ PQR, shown in the figure, the perpendicular PO drawn from P to base QR will be considered as the height of the triangle. Any side of the triangle may be taken or considered as the base.
If, QR is the base, and PO is height then the area of the triangle PQR (∆ PQR)
1
= ----------- QR X PO
2
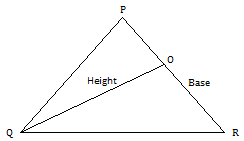
If, PR is the base of the triangle, then the area of a triangle is
1
= -------- X PR X QO
2
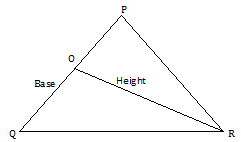
If, PQ is the base of the triangle, then the
area of a triangle is
1
= --------- X PQ X RO
2
2) We can also find the area of a triangle by Heron’s formula. According to this formula, if a, b, and c are the three sides of a triangle then
Area of a triangle = √s(s-a)(s-b)(s-c)
Where 2s = the perimeter of the triangle = a + b + c
a + b + c
Or, s = --------------
2
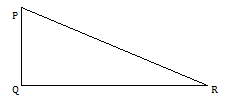
3) If PQR is a right angled triangle in which ∠B = 90⁰,
1 1
It’s area = ------- X base X height = ------- X QR X PQ
2 2
Area of the right angled triangle =
1------- X product of sides containing the right angle
2
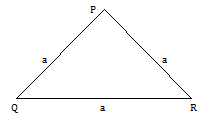
4) If PQR is an equilateral triangle,
a = b = c
a + b + c a + a + a 3a
s = ------------- = ------------- = ---------
2 2 2
So, area of ∆ PQR =
3a 3a 3a 3a
= √------ X (------ - a) X (------ - a) X (------ - a)
2 2 2 2
3a 3a – 2a 3a – 2a 3a – 2a
= √----- X (----------) X (----------) X (----------)
2 2 2 2
3a a a a
= √------- X ------- X -------- X --------
2 2 2 2
3 X a² X a² √3a²
= √--------------- = ---------
2² X 2² 4
√3
So, area of an equilateral triangle = --------- X (Side)²
2