CLASS-8
PROBLEM & SOLUTION OF TRIANGLE

Example.1) Find the area of a triangle in which the base is 8cm and the height 11cm.

Ans.) Here as per the given condition, the height of the triangle is 11cm and the base of the said triangle is 8cm.

As we all know the formula of- Area of a triangle = 1/2 X base X height

                                                                                    So, Area of a triangle = 1/2 X base X height

                                              1

                         = ------ X 8cm X 11cm =  44 cm²   (Ans.)

                              2                                                                       

Example.2) Find the area of a triangle of sides 42cm, 39cm, and 45cm. also find the length of the perpendicular from the vertex opposite the side of the length 42cm.

Ans.) let the triangle be ABC and let a = 42cm, b = 39cm, and c = 45cm 

               a + b + c        42 + 39 + 45          126          

Then, s = ------------ = --------------- = --------- =  63 cm

                  2                    2                  2

As we know the formula of Area of a triangle = √s(s-a)(s-b)(s-c)

So, Area of a triangle =  √63 X (63 – 42) X (63 – 39) X (63 – 45)

                         =  √63 X 21 X 24 X 18

                         =  √7 X 9 X 3 X 7 X 4 X 3 X 2 X 9 X 2

                         =  √ 7² X 9² X 3² X 4² 

                         =  7 X 9 X 3 X 4 = 756 cm

 

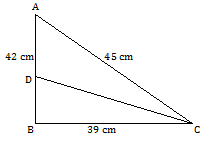
Let, CD is the perpendicular on base AB from the point C







                                                                                                                         1

Then, the area of triangle ABC = ------- X base X height 

                                         2

                      1

                = --------  X AB X CD

                      2                                                

                    1

Or, 756 cm = -------- X 42 X CD

                    2

Or,  21 CD =  756  

Or,   CD = 756/21 = 36 cm

Hence, the length of the perpendicular CD on AB from the point C = 36cm   (Ans.)

Example.3) Find the perimeter of an equilateral triangle of area 64√3 m²

Ans.) Let each side of the triangle = a m                                                                                                                 

 As we know that, as per the rules – 

                                                            √3

Area of an equilateral triangle = ------- X (side)²

                                        4

                            √3                    √3  

     =>     64√3 m² = ------- X (a m)² = ------ X a² m²

                             4                     4

     =>    64 X 4  =  a²

     =>    a  =  √8² X 2² =  16 m          (Ans.)