CLASS-8
DIAGONALS OF RECTANGLE & SQUARE

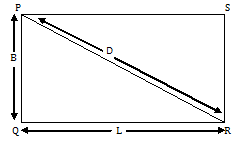
Let ‘D’ be the length of the diagonal PR of a rectangle PQRS, length (L) and breadth (B).

Then in the right angled triangle PQR, 

                        PR² =  PQ² + QR²

                       PR  =  √(PQ² + QR²)

                            =  √(breadth)² + (length)² = √B² + L²

Since the diagonals of a rectangle are equal.

Diagonal of a Square –

Let ‘D’ be the length of the diagonal PR of the square PQRS. Then, in the right-angled triangle PQR

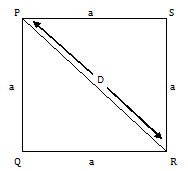
As per the Pythagoras theorem  PR² =  PQ² + QR²

From the above picture image PR = D, and  PQ = QR = RS = PS = a

       PR² =  PQ² + QR² 

Or,  D² =  a² + a²  = 2a²

Or,  D  =  √(2a²) =  √2a

Since the diagonals of a square are equal,

  Length of a square’s diagonal = √2 X any one side of square

There are some example are given below –

Example.)  If the diagonal and length of a rectangle are 10 cm and 8 cm respectively, find its (a) breadth, (b) perimeter, and (c) area.

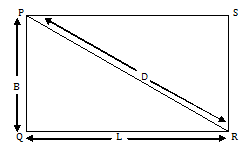
Ans.)  Given, D = 10 cm,

and L = 8 cm                                     

Let, breadth = B                

(a) as per the Pythagoras theorem we know -                                                                                                          

            D² =  B² +  L²

            B  = √(D²- L²) = √(10²- 8²) = √(100 - 64) 

                                             = √36 = √6² = 6 cm    (Ans.)