CLASS-8
DIAGONAL OF A CUBOID
DIAGONAL OF A CUBOID -
A diagonal of a cuboid is a line segment joining two vertices that are not on the same face. A cuboid has four diagonals (these said diagonals are also called principal diagonals).
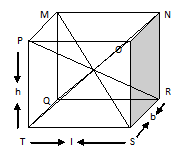
From the above picture or image following diagonal TN, QO, MS, PR. All these diagonals are considered to be equal in length. Let us find the length of HC.
In the rectangle QSOM, QO is the diagonal.
So, QO² = QS² + OS²
Now, QS is the diagonal of the rectangle TSRQ
QS² = TS² + QT² = l² + b²
So, QO² = QS² + OS² = l² + b² + OS²
= l² + b² + h²
QO = √(l² + b² + h²)
So, the length of a diagonal of a cuboid = √(l² + b² + h²)
Example) The dimensions of a cuboid are 10 cm, 20 cm, and 15 cm. Find the length of a diagonal.
Ans.) As per the given condition, l = 10 cm, b = 20 cm, h = 15 cm
As per the formula, the length of a diagonal of a cuboid
= √(l² + b² + h²)
= √(10² + 20² + 15²)
= √(100 + 400 + 225)
= √ 725
= 26.92 cm (approximately) (Ans.)