CLASS-8
CIRCUMFERENCE & AREA OF A CIRCLE
CIRCLE –
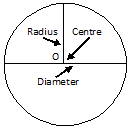
A circle is considered as the set of all points in a plane that are considered at a constant distance from a fixed point will be called the center of the circle. The constant distance will be considered as the radius of the circle, and a diameter of a circle will be considered as twice of its radius.
Circumference of a Circle –
The length of the entire arc of a circle will be called its circumference. The ratio of the length of the circumference (C) to the diameter (D) is considered as the same for all circles. We represent this ratio by Pi and the symbol of the Pi is denoted by π.
Where, Circumference (C), Diameter (D)
So,
Circumference (C) : Diameter (D) = Pi (π)
So, C : D = π
C
=> ------- = π , C = D π [ where π = 22/7 = 3.1416 approx. ]
D
Since, Diameter (D) = 2 X radius
So, C = 2 πr
Area Of Circle –
The area of a circle is considered by the measurement of the region bounded by the circle. The relationship between the area (A) and the radius (r) of a circle is as follows.
A = πr²
Or, r = √ A / π
There are some different formulas of circles given below for calculation- 1
The area of a semicircular region of radius (r) = ----- πr²
2
If the radii of two concentric circles (considered as, circles with the same center) are r & R, r < R then
The area of the ring (or annulus) = πR² - πr²
= π ( R² - r² )
= π (R + r) (R – r)