CLASS-8
AREA OF PARALLELOGRAM
Area of Parallelogram –
Let, PQRS be a parallelogram. Let us draw the rectangle XQRY on the same base and between the same parallels as the parallelogram PQRS.
Then, the area of the parallelogram PQRS
= the area of a rectangle XQRY
= QR X RY = base X height
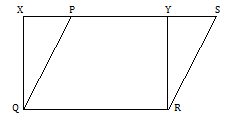
We can take any of the sides as the base and multiply it by the corresponding height. For example, if we take QR as a base, the corresponding height will be PY.
The area of a parallelogram = base X height
Also, since each diagonal of a parallelogram divides it into two congruent triangle
The area of parallelogram PQRS
= 2 X area of (∆ PQR) = 2 X area of (∆ SPR)
Example.) A parallelogram has adjacent sides of 30 cm and 40 cm. if the distance between the longer sides in 20 cm, find (a) the area of the parallelogram and (b) the distance between the shorter sides.
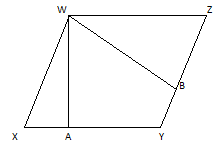
Let, WXYZ be the parallelogram.
Here, XY = WZ = 40 cm, XW = YZ = 20 cm, and distance between XY and WZ, that is AW = 10 cm
(a) area of the parallelogram = base (XY) X height (AW)
= 40cm X 10cm = 400 cm²
(b) let AW, the distance between the shorter sides XW & YZ = a cm
Then the area of parallelogram = base (YZ) X height (BW)
400 cm² = 20 cm X a
Or, a = 400 cm²/ 20 cm = 20 cm (Ans.)