CLASS-8
ANGLES OF POLYGON
ANGLES OF POLYGON
If we extend the side AF to X, we get the exterior angle EFX at the vertex F, and if we extend the side EF to Y, we get the exterior angles AFY at F, and ∠EFX = vertically opposite ∠AFY.
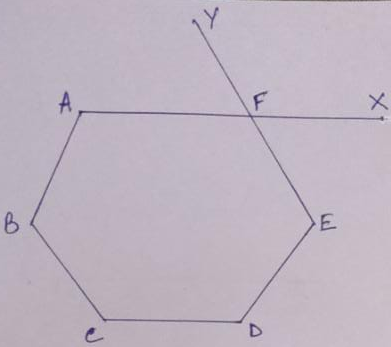
Also, ∠EFX + ∠EFA = ∠AFY + ∠EFA = 180⁰
We can generalize this for any polygon s follows –
1) at each vertex of a polygon, there are two equal exterior angles.
2) The sum of an exterior angle and adjacent interior angles at a vertex = 180⁰
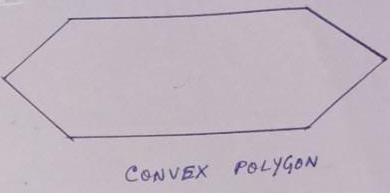
Convex Polygon –
If all the interior angles of a polygon are less than 180⁰, the polygon is said to be convex. All regular polygons are convex.

Concave (or re-entrant) polygon –
If one or more number of the interior angles of a polygons is greater than 180⁰ (that is, a reflex angle), the polygon should be considered as concave.