CLASS-8
ANGLE PROPERTIES OF A POLYGON
ANGLE PROPERTIES OF A POLYGON -
Properties.1) The sum of the Interior angles of a polygon with ‘n’ sides is considered as = (2n – 4) Right Angles.
For your better understanding, there are some examples are given below –
Example.1- The sum of the interior angles of a triangle = (2 X 3 – 4) right angles = 2 right angles = 180⁰, which is known to be true
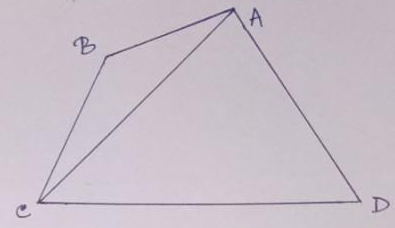
Example.2- The sum of the interior angles of a quadrilateral = (2n – 4) right angle
= (2 X 4 – 4) right-angle = 4 right angles
In the adjoining figure, the sum of the angles of the quadrilateral ABCD = the sum of the angles of ∆ BAC + the sum of the angles of ∆ ADC = 2 right angles + 2 right angles = 4 right angles.
So, it can be concluded that the property is true for a quadrilateral
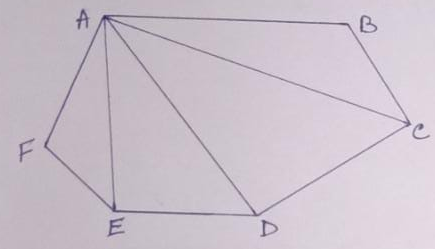
Example.3- The sum of the interior angles of a Hexagon = (2n – 4) right angle
= (2 X 6 – 4) right-angle = 8 right angles
In the adjoining figure, the sum of the angles of the hexagon ABCDEF = the sum of the angles of a triangles AFE, AED, ADC, and ACB = 4 X 2 right angles = 8 right angles
So, the property holds for a hexagon and it can be verified easily that it holds for other polygons as well.
Properties.2) The sum of the exterior angles of a convex polygon = 360⁰
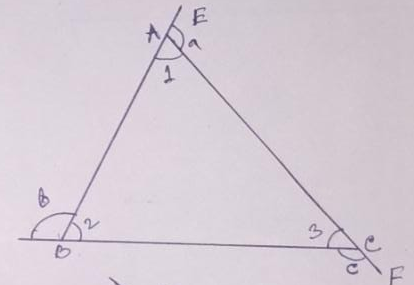
Example.1) In the adjoining figure,
∠a + ∠1 = 180⁰, ∠b + ∠2 = 180⁰, ∠c + ∠3 = 180⁰
∠a + ∠1 + ∠b + ∠2 + ∠c + ∠3 = 180⁰ + 180⁰ + 180⁰ = 540⁰
=> ∠a + ∠b + ∠c + ∠1 + ∠2 + ∠3 = 540⁰
=> ∠a + ∠b + ∠c + (∠1 + ∠2 + ∠3) = 540⁰
But, ∠1 + ∠2 + ∠3 = 180⁰, being angles of a triangle.
So, ∠a + ∠b + ∠c = 540⁰ - 180⁰ = 360⁰
So, the property is true for a triangle.
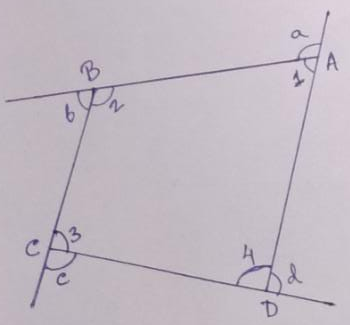
Example.2) In the adjoining figure,
∠a + ∠1 = 180⁰, ∠b + ∠2 = 180⁰, ∠c + ∠3 = 180⁰, ∠d + ∠4 = 180⁰
So, ∠a + ∠1 + ∠b + ∠2 + ∠c + ∠3 + ∠d + ∠4 = 180⁰ + 180⁰ + 180⁰ + 180⁰
So, ∠a + ∠b + ∠c + ∠d + (∠1 + ∠2 + ∠3 + ∠4) = 720⁰
But, the sum of the interior angles of a quadrilateral = 360⁰
So, ∠a + ∠b + ∠c + ∠d + 360⁰ = 720⁰
So, ∠a + ∠b + ∠c + ∠d = 720⁰ - 360⁰ = 360⁰
So, the property holds for a quadrilateral.
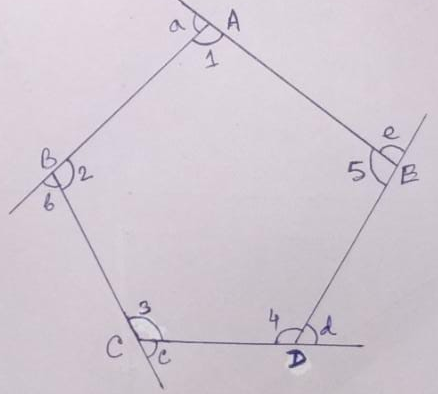
Example.3) In the adjoining figure,
∠a + ∠1 = 180⁰, ∠b + ∠2 = 180⁰, ∠c + ∠3 = 180⁰, ∠d + ∠4 = 180⁰, ∠e + ∠5 = 180⁰
So, ∠a + ∠1 + ∠b + ∠2 + ∠c + ∠3 + ∠d + ∠4 + ∠e + ∠5 = 180⁰ + 180⁰ + 180⁰ + 180⁰ + 180⁰
So, ∠a + ∠b + ∠c + ∠d + ∠e + ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 900⁰
So, ∠a + ∠b + ∠c + ∠d + ∠e + (∠1 + ∠2 + ∠3 + ∠4 + ∠5) = 900⁰
But, the sum of interior angles of a pentagon
= (2 X 5 – 4) right angles = 6 X 90⁰ = 540⁰
So, ∠a + ∠b + ∠c + ∠d + ∠e + (∠1 + ∠2 + ∠3 + ∠4 + ∠5) = 900⁰
So, ∠a + ∠b + ∠c + ∠d + ∠e + 540⁰ = 900⁰
So, ∠a + ∠b + ∠c + ∠d + ∠e = 900⁰ - 540⁰ = 360⁰
So, the property is true for the pentagon.
We can easily verify that the property holds for other polygons as well.