CLASS-8
FINDING SQUARE ROOT BY DIVISION METHOD
Finding Square Root By Division Method
Step.1) First, we have to make the pair of the digits of the given numbers from right to left, if the number of digits is odd then one digit will be left as unpaired at the extreme left of the given number. Now we will consider or put a small line segment over each pair of digits.
Step.2) Now we would consider the first pair of digits ( for odd digit number, we will consider the single unpaired digit first ) from the left end. This is to be considered as dividend. Now we have to recall or find the greatest number the square of which is not more than the a dividend. Write this number in the place of the quotient.
Step.3) Now we have to write or put a square of the number obtained in step.2 below the dividend and subtract and find the remainder (if any).
Step.4) Now we have to put or write the reminder obtained in Step.3 along with the next pair of digits of the given number. This new number would be the new dividend. If there is no reminder in Step.3, write only the next pair of digits of the given number.
Step.5) Now we have to write the first quotient just below the divisor and add them.
Step.6) Write the largest possible digit on the right of the sum (obtained in Step.5) so that the product of the new number and the largest possible digit does not exceed the new dividend. Subtract it from the new digit does not exceed the new dividend. Subtract it from the new dividend. This largest possible digit will be the second digit of the square root of the given number.
Step.7) Now we will write the remainder ( if any ) obtained in Step.6 along with the next pair of digits of the given number. This number would be considered as a new dividend.
Repeat the all the above-said process till all the pairs of the given number are exhausted.
For your better understanding, we would like to provide some example which given below -
1) Find the square root of 39204
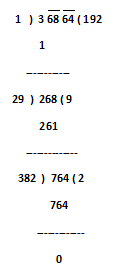
Step.1) Make the pairs of digits, these are 68 & 64 but 3 is an unpaired digit
Step.2) The greatest number the square of which does not exceeds 3 is 1. Write 1 in the quotient place.
Step.3) Write 1²= 1 below 3 and subtract, obtained reminder is 2
Step.4) So, now we will put the first pair digit 68 just after obtained reminder 2. So the new dividend is 268.
Step.5) So, now multiply 2 with quotient 1 and we obtained the product 2 which will be considered as the divisor and this is to be placed or put in divisor position.
Step.6) The largest possible digit that can be written next to 2 such that the product of the new number and that digit does not exceed 268 is 9, write 9 next to 1 in the quotient place.
Step.7) Write 9 X 29 = 261 below the dividend and subtract. Now we have a reminder, which is 7.
Step.8) So, now we will put second pair digit 64 just after obtained reminder 7. So the new dividend is 764.
Step.9) So, now multiply 2 with quotient 19 and the obtained product 38 which will be considered as divisor and to be placed or put in divisor position.
Step.10) The largest possible digit that can be written next to 38 such that the product of the new number and that digit does not exceed 764 is 2, write 2 next to 19 in the quotient’s place.
Step.11) Write 2 X 382 = 764 below the dividend and subtract. As we have no reminder after this, our work ends here.
So, √36864 = √192² = 192 (Ans.)
2) Find the square root of 55225
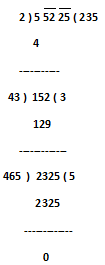
Step.1) Make the pairs of digits, these are 52 & 25 but 5 is an unpaired digit.
Step.2) The greatest number the square of which does not exceeds 5 is 2. Write 2 in the quotient place.
Step.3) Write 2² = 4 below 5 and subtract, obtained reminder is 1
Step.4) So, now we will put the first pair digit 52 just after obtained reminder 1. So the new dividend is 152.
Step.5) So, now multiply 2 with quotient 2 and we obtained the product 4 which will be considered as the divisor and this is to be placed or put in divisor position.
Step.6) The largest possible digit that can be written next to 4 such that the product of the new number and that digit does not exceed 152 is 3, write 3 next to 2 in the quotient’s place.
Step.7) Write 3 X 43 = 129 below the dividend and subtract. Now we have a reminder, which is 23.
Step.8) So, now we will put second pair digit 25 just after obtained reminder 23. So the new dividend is 2325.
Step.9) So, now multiply 2 with quotient 23 and the obtained product 46 which will be considered as divisor and to be placed or put in divisor position.
Step.10) The largest possible digit that can be written next to 46 such that the product of the new number and that digit does not exceed 2325 is 5, write 5 next to 23 in the quotient’s place.
Step.11) Write 5 X 465 = 2325 below the dividend and subtract. As we have no reminder after this, our work ends here.
So, √55225 = √235² = 235 (Ans.)
3) Find the square root of 425104
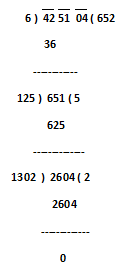
Step.1) Make the pairs of digits, these are 42, 51, & 04.
Step.2) The greatest number the square of which does not exceeds 42 is 6. Write 6 in the quotient place.
Step.3) Write 6² = 36 below 42 and subtract, obtained reminder is 6.
Step.4) So, now we will put second pair digit 51 just after obtained reminder 6. So the new dividend is 651.
Step.5) So, now multiply 2 with quotient 6 and we obtained the product 12 which will be considered as the divisor and this is to be placed or put in divisor position.
Step.6) The largest possible digit that can be written next to 12 such that the product of the new number and that digit does not exceed 651 is 5, write 5 next to 6 in the quotient place.
Step.7) Write 5 X 125 = 625 below the dividend and subtract. Now we have a reminder, which is 26.
Step.8) So, now we will put third pair digit 04 just after obtained reminder 26. So the new dividend is 2604.
Step.9) So, now multiply 2 with quotient 65 and the obtained product 130 which will be considered as divisor and to be placed or put in divisor position.
Step.10) The largest possible digit that can be written next to 65 such that the product of the new number and that digit does not exceed 2604 is 2, write 2 next to 65 in the quotient place.
Step.11) Write 2 X 1302 = 2604 below the dividend and subtract. As we have no reminder after this, our work ends here.
So, √425104 = √652² = 652 (Ans.)
4) Find the square root of 2304
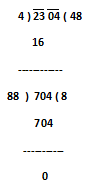
Step.1) Make the pairs of digits, these are 23 & 04.
Step.2) First consider 1st pair, the greatest number the square of which does not exceed 23 is 4. Write 4 in the quotient place.
Step.3) Write 4² = 16 below 23 and subtract, obtained reminder is 7.
Step.4) So, now we will put 2nd pair digit 04 just after obtained reminder 7. So the new dividend is 704.
Step.5) So, now multiply 2 with quotient 4 and we obtained the product 8 which will be considered as the divisor and this is to be placed or put in divisor position.
Step.6) The largest possible digit that can be written next to 8 such that the product of the new number and that digit does not exceed 704 is 8, write 8 next to 4 in the quotient place.
Step.7) Write 8 X 88 = 704 below the dividend and subtract. As we have no reminder after this, our work ends here.
So, √2304 = √48² = 48 (Ans.)