CLASS-8
SQUARE ROOT OF NON-PERFECT SQUARE NATURAL NUMBER

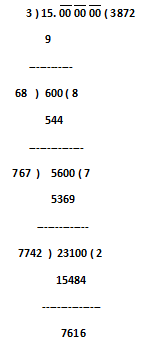
Step.1)  First to find out square root off 15, we would like to place a decimal point after 15 and then put three pairs of zeros ‘0’ ( zero after decimal place have no value or not define any value ) after decimal point. Now we would like to make the pairs of digits of obtained number 15.000000, the pairs of digits, these are 15, 00, 00, & 00.

Step.2)  The greatest number the square of which does not exceeds 15 is 3. Write 3 in the quotient place.

Step.3) Write 3² = 9 below 15 and subtract, obtained reminder is 6.

Step.4) So, now we will put the first pair digit 00 just after obtained reminder 6. So the new dividend is 600.

Step.5)  So, now multiply 2 with quotient 3 and we obtained the product 6 which will be considered as the divisor and this is to be placed or put in divisor position.

Step.6) The largest possible digit that can be written next to 6 such that the product of the new number and that digit does not exceed 600 is 8, write 8 next to 3 in the quotient place.

Step.7) Write 8 X 68 = 544 below the dividend and subtract. Now we have a reminder, which is 56.

Step.8) So, now we will put second pair digit 00 just after obtained reminder 56. So the new dividend is 5600.

Step.9) So, now multiply 2 with quotient 38 and the obtained product 76 which will be considered as divisor and to be placed or put in divisor position.

Step.10) The largest possible digit that can be written next to 76 such that the product of the new number and that digit does not exceed 5600 is 7, write 7 next to 38 in the quotient’s place.

Step.11) Write 7 X 767 = 5369 below the dividend and subtract. We find the reminder 231

Step.12) So, now we will put second pair digit 00 just after obtained reminder 231. So the new dividend is 23100.

Step.13) So, now multiply 2 with quotient 387 and the obtained product 774 which will be considered as divisor and to be placed or put in divisor position.

Step.14) The largest possible digit that can be written next to 774 such that the product of the new number and that digit does not exceed 23100 is 2, write 2 next to 387 in the quotient’s place.

Step.15) Write 2 X 7742 = 15484 below the dividend and subtract. We find the reminder 7616, and the process continues…… as per the zero you have entered after decimal places.

Step.16) The decimal point is placed in the quotient when the first pair of the digits of the decimal part is written in the dividend.

Now, after placement decimal point the obtained quotient would be 3.872 and correct to two decimal places the required number would be = 3.87

  So, √15 = √3.87² = 3.87   (Ans.)

Example.2)  Find out the square root of 19

Answer) Suppose given number 19 is to be arranged like 19.000000

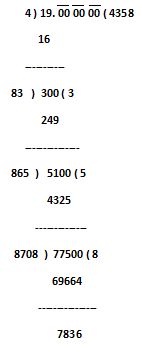
Step.1)  First to find out square root off 19, we would like to place a decimal point after 19 and then put three pairs of zeros ‘0’ ( zero after decimal place have no value or not define any value ) after decimal point. Now we would like to make the pairs of digits of obtained number 19.000000, the pairs of digits, these are 19, 00, 00, & 00.

Step.2)  The greatest number the square of which does not exceeds 19 is 4. Write 4 in the quotient place.

Step.3)  Write 4² = 16 below 19 and subtract, obtained reminder is 3.

Step.4)  So, now we will put the first pair digit 00 just after obtained reminder 3. So the new dividend is 300.

Step.5)  So, now multiply 2 with quotient 4 and we obtained the product 8 which will be considered as the divisor and this is to be placed or put in divisor position.

Step.6) The largest possible digit that can be written next to 8 such that the product of the new number and that digit does not exceed 300 is 3, write 3 next to 4 in the quotient place.

Step.7) Write 3 X 83 = 249 below the dividend and subtract. Now we have a reminder, which is 51.

Step.8) So, now we will put second pair digit 00 just after obtained reminder 51. So the new dividend is 5100.

Step.9) So, now multiply 2 with quotient 43 and the obtained product 86 which will be considered as divisor and to be placed or put in divisor position.

Step.10) The largest possible digit that can be written next to 86 such that the product of the new number and that digit does not exceed 5100 is 5, write 5 next to 43 in the quotient’s place.

Step.11) Write 5 X 865 = 4325 below the dividend and subtract. We find the reminder 775.

Step.12) So, now we will put second pair digit 00 just after obtained reminder 775. So the new dividend is 77500.

Step.13) So, now multiply 2 with quotient 435 and the obtained product 870 which will be considered as divisor and to be placed or put in divisor position.

Step.14) The largest possible digit that can be written next to 870 such that the product of the new number and that digit does not exceeds 77500 is 8, write 8 next to 435 in the quotient’s place.

Step.15) Write 8 X 8708 = 69664 below the dividend and subtract. We find the reminder 7836, and the process continues…… as per the zero you have entered after decimal places.

Step.16) The decimal point is placed in the quotient when the first pair of the digits of the decimal part is written in the dividend.

Now, after placement decimal point the obtained quotient would be 4.358 and correct to two decimal places the required number would be = 4.36

  So, √19 = √4.36² = 4.36   (Ans.)