CLASS-7
RELATION BETWEEN HCF & LCM

Relation between HCF & LCM 

HCF X LCM = First Number X  Second Entertainment

From the above equation, we can conclude that, the product of two numbers is equal to the product of their HCF & LCM and the

HCF of the two numbers can’t be greater than any of the given numbers.

HCF of two co-prime numbers = 1

The LCM of two co-prime numbers = the product of the numbers

LCM of two numbers cannot be less than any of the given numbers

Example – 1

The LCM & HCF of the two numbers is 336 &  28 respectively. If one number is 112 then find out the other number

Ans.) As per the given condition formula is  HCF X LCM = First Number X Second Entertainment

                             HCF X LCM 

So, Required number = ---------------

                            Given number

                               336   X   28

So, Required number =  -----------------   =  84    (Ans.)

                                   112

Example.– 2

If the product of two number is 23814 and their LCM is 378 then find their HCF

Ans.) as per the given condition –

1^st Number X 2^nd Number = HCF X LCM

               1^st Number X 2^nd Number           23814

=>  HCF  = ------------------------  =  -----------  =  63

                         LCM                          378

So, the required LCM is 63

Example– 3

Find the smallest number which when divided by 25, 40, 80, 120 leaves the remainder 11 in each case.

Ans.) The smallest number divisible by 25, 40, 80, 120 = the LCM of 25, 40, 80, 120.  

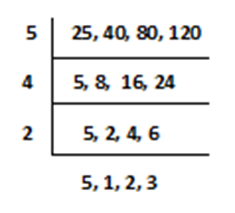
So, LCM of the numbers 25, 40, 80, 120 is  5 X 4 X 2 X 5 X 2 X 3 X 1 = 1200

So, as per the given condition the required number must be = obtained LCM from given numbers + 11 = 1200 + 11 = 1211   (Ans.)

Example- 4

Find the greatest number of 6 digits which is exactly divisible by  10, 20, 25, 35, 40.

First, we have to find LCM of  10, 20, 25, 35, 40  

So, the LCM of  10, 20, 25, 35, 40 =  5 X 2 X 2 X 5 X 7 X 2 = 1400

The greatest six-digit number is  = 999999. Let us see if it is a multiple of 1400

Consider 1400 as divisor and 999999 as dividend.

Here the remainder is 399. So, the number would be  999999 – 399 = 999600  (Ans.)

Example– 5

Find the smallest number of six digits which is exactly divisible by 10, 20, 25, 35, 40.

First, we have to find LCM of  10, 20, 25 , 35, 40  

So, the LCM of  10, 20, 25, 35, 40 = 5 X 2 X 2 X 5 X 7 X 2 = 1400

The smallest six-digit number is = 100000.

Let us see if it is a multiple of 1400.

Consider 1400 as divisor and 100000 as dividend

So, the required numbers =

   100000 – Remainder + LCM  

 = 100000 – 600 + 1400

 =  100800    (Ans.)