CLASS-7
INTRODUCTION OF RATIO
RATIO
The ratio of two quantities x & y is the fraction x/y if the quantities are of the same kind and are measured using the same unit. Remember that the ratio of two quantities of different kinds it may be different types of unit which is length, time, or quantity these all are meaningless and the two quantities must be measured in the same unit.
The ratio of two numbers x & y is expressed as x : y and this is to be read as x to y, x, & y are called terms of ratio. x is the first term or ANTECEDENT and y is the second term or CONSEQUENT,
ANTECEDENT : CONSEQUENT
A ratio should not have any unit
If both the numbers or quantities of a ratio are multiplied or divided by the same number in spite of that the ratio is unaltered.
The ratio should be expressed in the lowest term, if the antecedent and the consequent of the ratio are integers, we should divide both by their HCF to express the ratio in the simplest form.
If the ANTECEDENT or the CONSEQUENT of a ratio is a fraction, we should multiply both by the LCM of their denominator.
Examples –
a) 20 : 50 = ( 20 ÷ 10) : ( 50 ÷ 10) = 2 : 5 [HCF of 20 & 50 is 10]
b) 12 : 48 = ( 12 ÷ 12 ) : ( 48 ÷ 12) = 1 : 4 [HCF of 12 & 48 is 12]
Find out the Ratio from given Fraction
5 3
c) --------- : --------
24 20
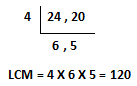
Step.1) First we have to find out LCM of both the denominator 24, 20
Step.2) Now we will divide the obtained LCM by Denominator of given fraction respectively.
120 ÷ 24 = 5 and 120 ÷ 20 = 6; here 5 & 6 are the quotient respectively
Step.3) Now, we will multiply by obtained quotient to denominator and numerator of the given fraction respectively
5 5 X 5 25
We find -------- = ------------ = --------
24 24 X 5 120
3 3 X 6 12
We find -------- = ------------ = ---------
20 20 X 6 120
5 3 25 18
So, -------- : -------- = -------- : -------- = 25 : 18
24 20 120 120
(Ans.)
Find Out the Ratio from given Fraction -
7 6
d) --------- : ---------
15 25
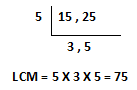
Step.1) First we have to find out LCM of both the denominator 24, 20.
Step.2) Now we will divide the obtained LCM by Denominator of given fraction respectively.
75 ÷ 15 = 5, and 75 ÷ 25 = 3; here 5 & 3 are the quotient respectively
Step.3) Now, we will multiply by obtained quotient to denominator and numerator of the given fraction respectively
7 7 X 5 35
We find -------- = ----------- = -------
15 15 X 5 75
6 6 X 3 18
We find -------- = ----------- = -------
25 25 X 3 75
7 6 35 18
So, ------ : ------ = ------- : ------- = 35 : 18 (Ans.)
15 25 75 75