CLASS-7
FINDING HCF BY DIVISION METHOD

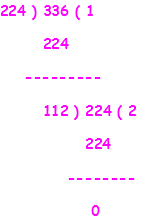
Step.1– we divide 336 by 224 and we find 112 as a reminder.

Step.2– We consider reminder 112 as Divisor and previously taken Divisor 224 would be considered as Dividend in the next step.

Step.3– we divide Dividend 224 by Divisor 112 and get Quotient 2 and reminder Zero ‘0’. The process would have continued until the reminder becomes zero ‘0’.

So, the HCF of two given numbers 224 & 336  would be 112.      (Ans.)

Example -2

Find the HCF of 308 & 420

Ans.) We take the smallest number between given numbers 308 & 420 as Divisor and another would be considered as Dividend. So, 308 is Divisor and 420 is Dividend to be considered – 

Step.1- We divide 420 by 308 and we find 112 as a reminder.

Step.2– We consider reminder 112 as Divisor and previously taken Divisor 308 would be considered as Dividend in the next step.

Step.3– We find 84 as a reminder and now 84 would be considered as Divisor and previously taken Divisor 112 would be considered as Dividend now. The same process will be repeated until the reminder to be found Zero ‘0’. 

Step.4 – We find 28 as a reminder and it is to be considered now as divisor and previously taken Divisor 84 would be considered as Dividend. 

Step.5– Now we find 3 as Quotient and obtained reminder is Zero ‘0’.

So, the HCF of two given numbers 308 & 420 would be 28  (Ans.)

Example– 3

Find the greatest number (HCF) of  528, 1296 & 1120

Ans.) We will take the two smallest numbers between given numbers 528, 1296 & 1120, so we will take 528 as Divisor and 1120 would be considered as Dividend. So, 528 is Divisor and 1120 is Dividend to be considered –

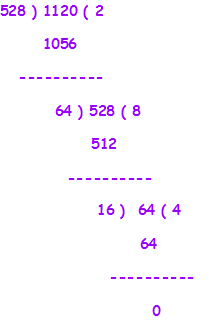
Step.1– We divide 1120 by 528 and we find 64 as a reminder.

Step.2– Now we consider 64 as a divisor and earlier divisor 528 to be considered as a dividend. Now we get 16 as a reminder.

Step.3– Now we consider 16 as Divisor and earlier divisor 64 to be considered as dividends. The same process will be continued until we find the reminder as Zero ‘0’

Step.4- Now we find quotient 4 and reminder zero ‘0’. The HCF of 528 & 1120 is = 16, now we will find the HCF between 16 & 1296.

Step.5– consider 16 as divisor and 1296 as dividend.

Step.6– here we find that, 81 as quotient and reminder is Zero ‘0’. 

The HCF of 16 & 1296 is 16, so the HCF of 528, 1296 & 1120 is 16.        (Ans.)

Example– 4

Find the greatest number (HCF) of 456, 2128 & 1140

Ans.) We will take the two smallest numbers between given numbers 456, 2128 & 1140 so we will take 456 as Divisor and 1140 would be considered as Dividend. So, 456 is Divisor and 1140 is Dividend to be considered –

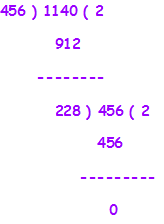
Step.1– We divide 1140 by 456 and find the reminder 228.

Step.2– Now, we consider reminder 228 as divisor and 456 as dividend and we Zero ‘0’ reminder. So, 228 is the HCF of 1140 & 456

The HCF of 456 & 1140 is = 228, now we will find the HCF between 228 & 2128

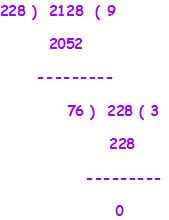
Step.3- We will take obtained HCF of 1140 & 456 which is 228 as divisor and consider 2128 as dividend and we find 76 as a reminder

Step.4 – We will consider reminder 76 as divisor and previous divisor 228 is considered as dividend and we found Zero ‘0’ as a reminder.

HCF of the numbers 228 & 2128 is 76.  (Ans.)