CLASS-7
ALGEBRA RULES FOR OPENING BRACKETS

The four type of Brackets used to group together in an Expression are –

1) vinculum or line bracket  ͞

2) first bracket ( )

3) second bracket { }

4) third bracket  [ ]

While simplifying an expression they should open in order  ͞  , ( ), {  }, [ ]

Rules for opening brackets –

1) If there is a positive sign outside the opening brackets then we remove the brackets without changing the signs of the terms within the bracket.

2) If there is a negative sign outside the opening brackets, we have to change the signs of all the terms within the brackets when we remove the bracket.

An Algorithm Expression can be Put within Brackets –

1) without changing the signs of the terms by keeping the positive sign immediately before the opening brackets.

2) by changing the sign of each term within brackets by keeping the negative sign immediately before the opening brackets.

Insertion of Brackets –

1) when we put terms within brackets with a positive sign outside the opening brackets, we place the terms within the brackets without changing the signs.

Example-  x – y + z  =  x + (- y + z ),  a – b – c = a + ( - b – c )

2) If we want to place an expression within brackets with a negative sign outside the opening balance, we must change the signs of all the terms within the brackets.

Example –

1)   x – y – z   = x – ( y + z )

2)   w – x – y – z  =  w – ( x + y + z )  =  w – { x + ( y + z )}

3)   w – x + y – z  =  w – ( x - y + z )  =  w – { x - ( y - z )}

Example.1)  Simplify 5x ( x + 3 ) – 2x

 Ans.)      5x ( x + 3 ) – 2x

         =  5x . x + 5x . 3 – 2x

         =  5 x¹⁺¹ + 15x – 2x

         =  5x² + 13x

Example.2)  Simplify 3x ( 5x² + 3y – z – 4 ) – 2y + 4x

Ans.)   3x ( 5x² + 3y – z – 4 ) – 2y + 4x

         =  3x . 5x² + 3x . 3y – 3x . z  - 3x . 4 – 2y + 4x

         =  15 x²⁺¹ + 9 x.y – 3xz – 12x – 2y + 4x

         =  15 xᶟ + 9xy – 3xz – (12 – 4).x  - 2y

         =  15 xᶟ + 9xy – 3xz – 8x - 2y

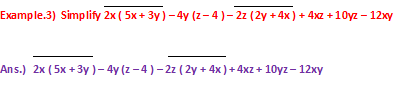
As per the rules if there is “Vinculum” or “Line Bracket”, then we have take the action first in that region of the given calculation.

 =  ( 2x . 5x + 2x . 3y ) – 4y (z – 4) - ( 2z . 2y – 2z . 4x ) + 4xz + 10yz – 12xy

 =  10 x¹⁺¹ + 6 x . y – 4y (z – 4) – 4 y . z + 8 x . z + 4xz + 10yz – 12xy

 =  10 x² + 6 xy – 4yz + 16y – 4yz + 8xz + 10yz – 12xy

 =  10 x² - ( 12 – 6 ) xy – ( 4 + 4 – 10 ) yz + 16y + 8xz

 =  10x² - 6xy – ( - 2 ) yz + 16y + 8xz

 =  10x² - 6xy + 2yz + 16y + 8xz