CLASS-6
SET - UNION OF SETS

UNION OF SETS -

The union of two sets, denoted by A∪B, is a new set that contains all the distinct elements that are in either set A or set B, or in both.

Formally, for two sets A and B, the union is defined as:

A∪B = {x : x ∈ A or x ∈ B}

Example.1) Here's an example to illustrate:

Let's say we have two sets:

A = {1, 2, 3} and B = {3, 4, 5}.

The union of A and B would be:

  A∪B = {1, 2, 3, 4, 5}.

Notice that the element "3" is only counted once in the union, even though it appears in both sets.

Example.2)  For example, let's say we have two sets:

Set A = {1, 2, 3, 4} Set B = {3, 4, 5, 6}

The union of sets A and B, denoted as A ∪ B, will be:

A ∪ B = {1, 2, 3, 4, 5, 6}

Notice that any duplicate elements are only included once in the union.

The union operation is commutative, which means that the order of the sets does not matter. That is, A ∪ B is the same as B ∪ A.

It's also possible to take the union of more than two sets. For example, the union of three sets A, B, and C would be denoted as A ∪ B ∪ C and would include all the distinct elements from these three sets.

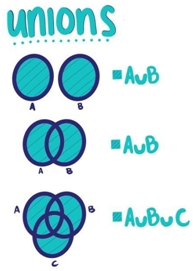
Additionally, you can take the union of more than two sets. For instance, if you have three sets A, B, and C:

A = {1, 2, 3}, B = {3, 4, 5}, and C = {5, 6, 7}

Then, the union of these three sets (A ∪ B ∪ C) will contain all the distinct elements from A, B, and C.

A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7}