CLASS-6
SET - DISJOINT SET
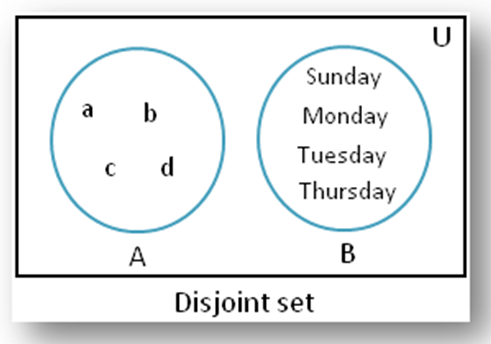
DISJOINT SET -
Disjoint sets, also known as mutually disjoint sets or pairwise disjoint sets, are sets that have no elements in common. In other words, two or more sets are disjoint if the intersection of any pair of sets results in an empty set.
Mathematically, if you have sets A, B, C, etc., they are said to be disjoint if:
A ∩ B = ∅ (the intersection of A and B is the empty set), A ∩ C = ∅ (the intersection of A and C is the empty set), B ∩ C = ∅ (the intersection of B and C is the empty set), and so on.
For example, consider the following two sets:
A = {1, 2, 3}, B = {4, 5, 6}
These sets are disjoint because their intersection is empty:
A ∩ B = ∅,
It's important to note that disjoint sets can refer to any number of sets, not just two. If you have three sets, A, B, and C, they are disjoint if:
A ∩ B = ∅ (no common elements between A and B), A ∩ C = ∅ (no common elements between A and C), B ∩ C = ∅ (no common elements between B and C).
In general, when multiple sets are disjoint, it means that there are no elements that appear in more than one of those sets. Disjoint sets are often used in various areas of mathematics and set theory, and they can be useful in solving problems involving set operations and relationships.
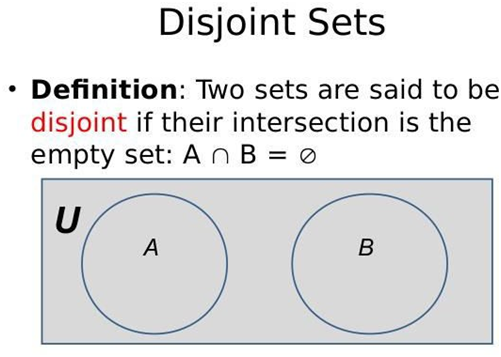
Disjoint sets, also known as mutually exclusive sets, are sets that have no elements in common. In other words, if two or more sets are disjoint, it means they do not share any elements.
For example, consider two sets:
Set A = {3, 4, 5, 6}, Set B = {7, 8, 9, 10, 11}
In this case, sets A and B are disjoint because they have no elements in common.
It's worth noting that the intersection of disjoint sets is always an empty set (∅), because there are no elements that are present in both sets.
Disjoint sets are commonly encountered in various branches of mathematics, including set theory, probability theory, and statistics. For example, when dealing with events in probability theory, two events are said to be mutually exclusive if they cannot both occur at the same time. This concept is fundamental in the calculation of probabilities.