CLASS-6
RECIPROCAL OF MULTIPLICATION OF INVERSE
RECIPROCAL OR MULTIPLICATION OF INVERSE -
If the product of the two fractions is 1, each fraction is called a reciprocal of each other.
X Y
When, ------- x -------
Y X
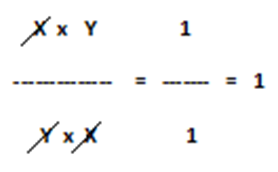
1
= ------- = 1
1
X Y
So, the reciprocal of -------- is -------- and vice versa
Y X
On the other wards, X / Y and Y / X are multiplicative inverses of each other.
The reciprocal of a fraction is obtained by interchanging the numerator and the denominator of the fraction. In other words, if you have a fraction "a/b," its reciprocal is "b/a." The reciprocal of a number is also known as its multiplicative inverse, meaning that when you multiply a number by its reciprocal, the result is 1.
For example, the reciprocal of the fraction 3/4 is 4/3. Similarly, the reciprocal of 5/6 is 6/5, and so on.
For example:
- The reciprocal of 2/3 is 3/2.
- The reciprocal of 5/8 is 8/5.
- The reciprocal of 1/4 is 4/1 (which is just 4).
Reciprocals are useful in various mathematical operations, such as dividing fractions or simplifying expressions.
1 9
Example- 1) Reciprocal of ------- is -------- = 9
9 1
15 1
2) Reciprocal of 15 = -------- is --------
1 15
15 7
3) Reciprocal of -------- is ---------
7 15
37 121
4) Reciprocal of --------- is ----------
121 37
147 22
5) Reciprocal of ---------- is ---------
22 147