CLASS-6
PRIME FACTORIZATION

PRIME FACTORIZATION -

Prime factorization is the process of expressing a positive integer as a product of its prime factors. A prime factor is a prime number that divides the original integer exactly without leaving a remainder.

factorization

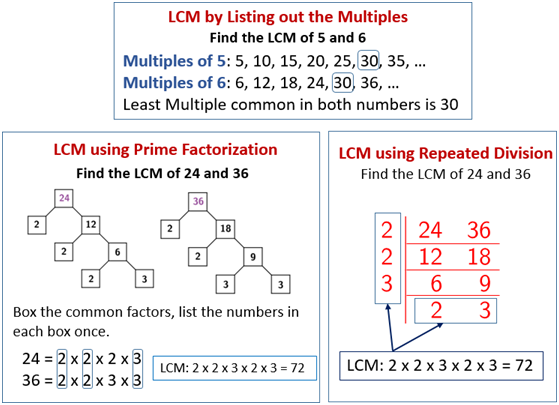
Here's how you can find the prime factorization of a number:

  1. Start by dividing the number by the smallest prime number (which is 2) and continue dividing by prime numbers until you cannot divide any further.
  2. Write down the prime factors as you find them.
  3. Repeat the process for the quotient obtained from the previous division until the quotient becomes 1.
  4. The product of all the prime factors you found is the prime factorization of the original number.

For example, let's find the prime factorization of the number 56:

  1. Divide 56 by the smallest prime number, which is 2: 56 ÷ 2 = 28.
  2. Divide 28 by 2: 28 ÷ 2 = 14.
  3. Divide 14 by 2: 14 ÷ 2 = 7.
  4. Since 7 is a prime number, we stop here.

The prime factorization of 56 is 2³ X 7.

Another Example:- Let's find the prime factorization of 120:

  1. Divide 120 by 2: 120 ÷ 2 = 60.
  2. Divide 60 by 2: 60 ÷ 2 = 30.
  3. Divide 30 by 2: 30 ÷ 2 = 15.
  4. Divide 15 by 3: 15 ÷ 3 = 5.
  5. Since 5 is a prime number, we stop here.

The prime factorization of 120 is 2³ X 3 X 5.

Prime factorization is important in various mathematical and computational applications, including finding the greatest common divisor (GCD) and least common multiple (LCM) of numbers, simplifying fractions, and solving certain types of equations.


Some Other way Of Understanding About "Prime Factorization",