CLASS-6
HIGHEST COMMON FACTOR (HCF)
HIGHEST COMMON FACTOR (H.C.F) OR GREATEST COMMON DIVISOR (G.C.D) –
The H.C.F or G.C.D of two or more numbers is the greatest number that divides each one of them exactly-
If we consider the number 24 and 36 then,
the factors of the 24 are = 1, 2, 3, 4, 8, 6, 12, 24
the factors of the 36 are = 1, 2, 3, 4, 6, 9, 12, 18, 36
so, common factors of the 24 and 36 are = 1, 2, 3, 4, 6, 12 and the greatest between these is 12
So, H.C.F or G.C.D of the two given numbers 24 & 36 is 12. (Ans.)
ANOTHER METHOD OF – FINDING H.C.F THROUGH PRIME FACTORISATION METHOD –
Find the H.C.F of 24 & 36
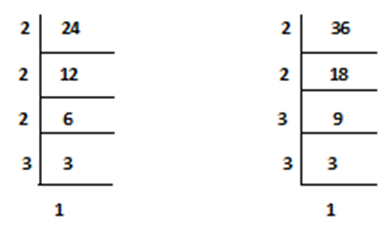
Step.1) Express each number which is to be considered as a product of prime factors.
Step.2) Find the common factors to all the numbers.
Step.3) The product of these common factors is the required H.C.F
24 = 2 x 2 x 2 x 3 x 1
36 = 2 x 2 x 3 x 3 x 1
The common factors of the given numbers are 2, 2, & 3.
So, H.C.F of 24 & 36 is = 2 x 2 x 3 = 12 (Ans.)
ANOTHER METHOD OF – FINDING H.C.F THROUGH LONG DIVISION METHOD –
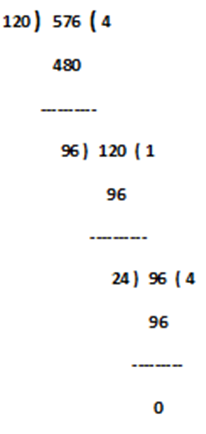
1) Find H.C.F of 120 and 576 by Long Division Method
Ans.) For finding the H.C.F of two given numbers by long division method, we should proceed according to the following steps are given below –

Step.1) Consider the greater number as ‘Dividend’ and smaller number as ‘ Divisor’, so, consider 576 as ‘Dividend’ and 120 as ‘Divisor’.
Step.2) Start division like normal division and you will find the remainder every time, and then again we have to divide ‘Divisor’ by ‘Remainder’. Here 96 is ‘Remainder’ and 120 is ‘Divisor’, as per the given communication we will divide 120 by 96 and the steps continue.
Step.3) Continue step 2 until the ‘Remainder’ becomes 0 (Zero). The last ‘Divisor’ is the desired H.C.F, so 24 is the H.C.F of both the numbers 120 & 576.
H.C.F OF THREE OR MORE NUMBERS –
1) Find H.C.F of 120, 576, and 444 by Long Division Method
Ans.) For finding the H.C.F of two given numbers by long division method, we should proceed according to the following steps are given below –
Step.1) Find H.C.F of any two of the given numbers and then find H.C.F of the third given number and the H.C.F number obtained from first two numbers.
Step.2) Take two numbers 120 & 576, consider the greater number as ‘Dividend’ and the smaller number as ‘ Divisor’, so, consider 576 as ‘Dividend’ and 120 as ‘Divisor’.
Step.3) Start division like normal division and you will find the remainder every time, and then again we have to divide ‘Divisor’ by ‘Remainder’. Here 96 is ‘Remainder’ and 120 is ‘Divisor’, as per the given communication we will divide 120 by 96 and the steps continue.
Step.4) Continue step 2 until the ‘Remainder’ becomes 0 (Zero). The last ‘Divisor’ is the desired H.C.F, so 24 is the H.C.F of both the numbers 120 & 576.
Step.5) Now, we have to find H.C.F through the division method of third given number 444 and H.C.F 24 obtained from two given numbers 120 & 576.
We will consider 24 as ‘Divisor’ and 444 as ‘Dividend

Step.6) we will continue Step.3 & Step.4, process of division method continues till ‘Remainder’ is 0 (Zero)
So, H.C.F of 24 & 444 is 12,
So, H.C.F of given three numbers 120, 576, 444 is 12. (Ans.)