CLASS-6
GEOMETRY - POINT OF CONCURRENCY

POINT OF CONCURRENCY -

A "point of concurrency" in geometry refers to a single point where multiple lines, segments, rays, or other geometric elements intersect or meet. These points of concurrency are often associated with specific types of geometric figures and constructions and are important in various geometric theorems and problem-solving.

Here are some common points of concurrency in geometry:

1. Incenter (Point of Angle Bisectors):-  In a triangle, the incenter is the point of concurrency of the angle bisectors. It is equidistant from all three sides of the triangle and is the center of the triangle's inscribed circle (incircle).
2. Circumcenter (Point of Perpendicular Bisectors):- The circumcenter is the point of concurrency of the perpendicular bisectors of the sides of a triangle. It is equidistant from all three vertices and is the center of the triangle's circumscribed circle (circumcircle).
3. Centroid (Point of Medians):-  In a triangle, the centroid is the point of concurrency of the medians. Each median connects a vertex to the midpoint of the opposite side. The centroid divides each median into two segments, with the segment closer to the vertex being twice as long as the other segment.
4. Orthocenter (Point of Altitudes):-  The orthocenter is the point of concurrency of the altitudes of a triangle. An altitude is a perpendicular line drawn from a vertex to the opposite side. The orthocenter may be inside, outside, or on the triangle, depending on the type of triangle.
5. Euler's Triangle Center (Point of Perpendicular Bisectors, Medians, and Altitudes):-  The Euler's triangle center is the point where the perpendicular bisectors of the sides, medians, and altitudes of a triangle intersect. It plays a role in various geometric properties of the triangle.
6. Incenter and Circumcenter of a Quadrilateral:-  In some quadrilaterals, such as cyclic quadrilaterals (quadrilaterals that can be inscribed in a circle), there are points of concurrency that are analogous to the incenter and circumcenter of triangles.
7. Napoleon's Theorem (Napoleon Points):-  In Napoleon's theorem, equilateral triangles are constructed externally on the sides of an arbitrary triangle. The points where these equilateral triangles meet are called Napoleon points or Fermat points.
8. Concurrent Lines in Coordinate Geometry:-  In coordinate geometry, lines given by various equations may intersect at points of concurrency. For example, the x-axis, y-axis, and a line might intersect at the origin (0, 0).

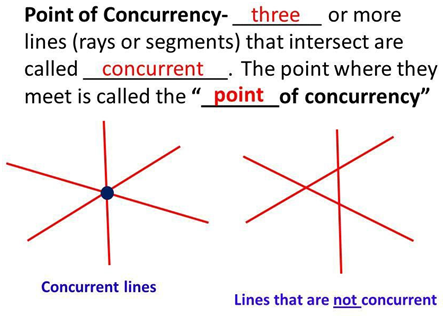
These points of concurrency often have geometric properties and relationships associated with them, and they are used in solving various types of geometric problems and proving theorems. Understanding points of concurrency can provide insights into the relationships between different elements in geometric figures.