CLASS-6
CONSTRACTION OF 60-DEGREE ANGLE
CONSTRACTION OF 60-DEGREE ANGLE -
To construct a 60-degree (60º)angle, you can follow these steps using a compass and a straightedge:
- Draw a Ray:- Start by drawing a ray (a straight line that extends indefinitely in one direction) using a straightedge. This ray will be the initial side of the angle.
- Place the Compass:- Place the compass on one endpoint of the ray, and open it to a convenient width. This width will be used to mark points on the ray.
- Draw an Arc:- With the compass set at the initial endpoint, draw an arc that intersects the ray. Let's call this point of intersection A.
- Without Changing the Compass Width:- Without changing the compass width, place the compass on point A and draw another arc that intersects the first arc. Let's call this point of intersection B.
- Draw the Angle:- Use a straightedge to draw a line connecting the initial endpoint of the ray to point B (the second intersection point).
The angle formed by the initial ray and the line connecting the two intersection points (A and B) is a 60-degree angle.
The reason this construction works is based on the properties of equilateral triangles. If you construct an equilateral triangle (a triangle with all sides equal), each angle will be 60 degrees. By constructing two congruent segments on the initial ray, you essentially create an equilateral triangle. The angle at the vertex is then 60 degrees.
Another Way Of Understanding -
We know that the angles in an equilateral triangle are all 60º in size. This suggests that to construct a 60º angle we need to construct an equilateral triangle as described below.
Step 1:- Draw the arm PQ.
Step 2:- Place the point of the compass at P and draw an arc that passes through Q.
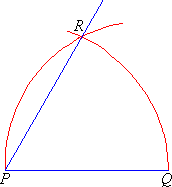
Step 3:- Place the point of the compass at Q and draw an arc that passes through P. Let this arc cut the arc drawn in Step 2 at R.
Step 4:- Join P & R. The angle QPR is 60º.