CLASS-6
CONSTRUCTION OF 135⁰ ANGLE
CONSTRUCTION OF 135 DEGREE (135⁰) ANGLE -
construct a 135-degree angle using a compass and straightedge, you can follow these steps:
- Draw a base line:- Start by drawing a straight line, which will be the base for your angle.
- Place the compass at one endpoint: Place the compass point (the sharp end) on one endpoint of the base line.
- Adjust the compass width:- Open the compass to a width greater than half the length of the base line. This will ensure that the arc you draw will intersect the base line on both sides.
- Draw an arc:- With the compass set, draw an arc that intersects the base line.
- Place the compass at the intersection point:- Place the compass point at the intersection point you just created on the base line.
- Draw another arc:- Without changing the compass width, draw another arc from the intersection point.
- Draw the angle bisector:- The intersection of the two arcs should form an angle bisector. Draw a straight line from the initial endpoint through the intersection point to the other side of the base line.
- Measure the angle:- The angle formed by the intersection of the base line and the bisector is 135 degrees.
This construction uses the properties of angles and bisectors to create a 135-degree angle. Make sure to use a ruler to draw straight lines and a compass to create accurate arcs.
Another Way Of Construction -
Steps Of Construction -
Step.1) Draw any straight line BA, and take a point O on it.
Step.2) With O as centre and suitable radius, draw an arc to cut the line.
Step.3) With B & A as centres, draw two arc of equal radius (>1/2 BA) cutting each other at C.
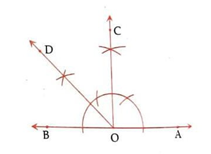
Step.4) Construct ∠COA = 90⁰, then ∠BOC = 90⁰.
Step.6) Bisect ∠BOC. Let ray OD be the bisector of ∠BOC, then ∠COD = 45⁰
So, ∠AOD = ∠AOC + ∠COD
= 90⁰ + 45⁰ = 135⁰