CLASS-6
GEOMETRY - COLLINEARITY OF POINTS

COLLINEARITY OF POINTS -

Collinearity of points is a geometric concept that describes a relationship between three or more points that lie on the same straight line. In other words, if three or more points are collinear, it means that they can be connected by a single straight line without any gaps or breaks. Here are some key points to understand about collinearity:

1. Definition:- Three or more points, A, B, and C, are said to be collinear if they all lie on the same straight line.
2. Non-Collinear Points:-  If three points do not lie on the same straight line, they are said to be non-collinear.
3. Collinear Points in Coordinate Geometry:-  In coordinate geometry, you can determine whether points are collinear by examining their coordinates. Three points (x₁, y₁), (x₂, y₂), and (x₃, y₃​​) are collinear if and only if the slopes of the line segments formed by connecting these points are equal. In other words, if the slopes of the lines AB, BC, and AC are equal, then A, B, and C are collinear.
4. Collinearity in Euclidean Geometry:-  In Euclidean geometry, you can establish collinearity by visually verifying that the points lie on the same straight line. This can be done by drawing a line through the points or by using a straightedge to check if a line can be drawn through all the points without any of them being off the line.
5. Use in Geometric Theorems:-  Collinearity is a fundamental concept in geometry and is used in various theorems and proofs. For example, the midpoint theorem states that the midpoint of a line segment is collinear with the endpoints of the segment.
6. Applications:-  Collinearity of points has practical applications in fields such as architecture, engineering, surveying, and computer graphics. It is essential for designing and analyzing structures, creating accurate diagrams, and solving geometric problems.

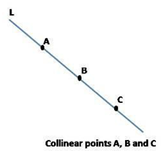
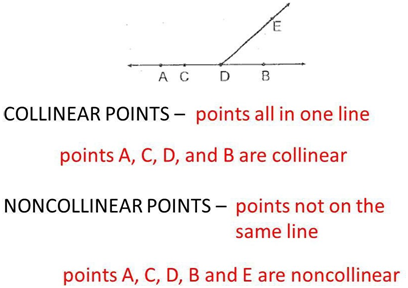
Overall, collinearity of points is a fundamental concept in geometry that helps describe the spatial relationships between points on a straight line. It is a concept that is widely used in various geometric contexts and has practical significance in many areas of science and engineering.