CLASS-6
COLIINEAR & NON-COLLINEAR POINT

COLIINEAR & NON-COLLINEAR POINT -

In geometry, the terms "collinear" and "non-collinear" are used to describe the spatial relationship between a set of points. These terms refer to whether the points lie on the same straight line or not. Let's define and explain both terms:

1. Collinear Points (Definition):- A set of points is said to be collinear if they all lie on the same straight line.In other words, if you can draw a single straight line that passes through all the points without any of them deviating from the line, those points are collinear.Collinear points can be connected by a single line segment, and they share the same line of action. For example, points A, B, C, and D are collinear if they all lie on the same line AB, or if a line segment can be drawn from A to D without leaving the line.
2. Non-Collinear Points (Definition):- A set of points is said to be non-collinear if they do not all lie on the same straight line.In other words, if you cannot draw a single straight line that passes through all the points without any of them being off the line, those points are non-collinear.Non-collinear points cannot be connected by a single line segment without introducing a curve or deviation from a straight path. For example, points A, B, C, and D are non-collinear if they are arranged in such a way that no single straight line can pass through all of them.

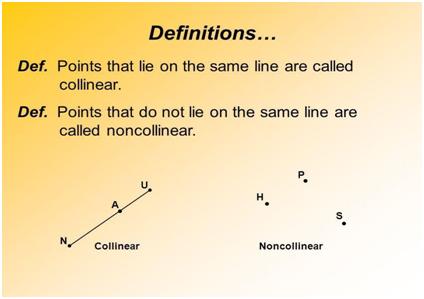
To determine whether a set of points is collinear or non-collinear, you can visually inspect the arrangement of the points or use mathematical methods, such as calculating slopes in coordinate geometry. Collinearity is a fundamental concept in geometry, and it is often used to describe relationships between points, lines, and shapes. Understanding collinearity is important for solving geometric problems and analyzing spatial configurations.