CLASS-6
TANGENT TO A CIRCLE
TANGENT TO A CIRCLE -
A tangent to a circle is a line that intersects the circle at exactly one point. In other words, it touches the circle at one point without crossing through it. This point of tangency is where the tangent line and the circle meet.
Here are some key points about tangents to circles:
- Point of Tangency:- The point where the tangent line touches the circle is called the point of tangency. At this point, the tangent is perpendicular to the radius of the circle.
- Perpendicularity:- At the point of tangency, the tangent line is perpendicular to the radius of the circle drawn to that point. This means that the radius and the tangent line form a right angle at the point of tangency.
- Slope:- The slope of a tangent line to a circle at a given point is equal to the negative reciprocal of the slope of the radius line passing through that point. This property helps in finding equations of tangent lines.
- Tangent-Secant Theorem:- If a tangent and a secant, or two secants, intersect at a point on a circle, then the measure of the angle formed is half the difference of the measures of the intercepted arcs.
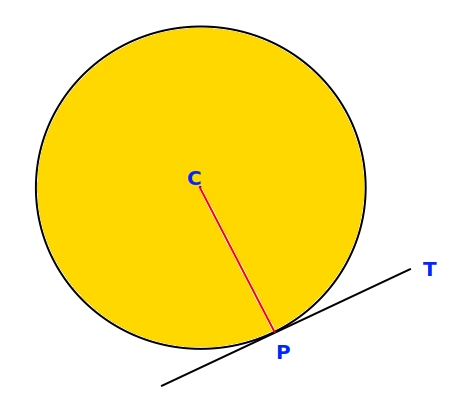
A line which meets a circle in one and only one point is called a tangent to the circle. In the above figure, the line PT is a tangent to the circle with centre C.
The point where the line meets (touches) the circle is called its point of contact.
Notice that, CP is perpendicular to PT.
Tangents play a crucial role in geometry, particularly in circles. They are used in various geometric proofs, constructions, and problem-solving scenarios. In real-world applications, tangents are utilized in fields such as optics, where they represent the direction of light rays as they graze the surface of a curved lens or mirror.