CLASS-6
SECTOR OF A CIRCLE

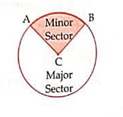
The part of the circular region of the plane enclosed by an arc of a circle and its two bounding radii is called a sector of the circle. The part containing the minor arc is called the minor sector, and the part containing the major arc is called the major arc.

In the above diagram, the part of the region of the plane enclosed by the minor arc AB and its two bounding radii CA & CB is minor sector of the circle with centre C, ∠ACB is called the angle of the sector. Usually the term "sector of a circle" is referred to the area of the region.

A sector is defined by its central angle and the radius of the circle. The area of a sector can be calculated using the formula:

                      Central Angle

Area of Sector= --------------- X πr2

                          360∘

Where:

• Central Angle is the angle in degrees that the sector subtends at the centre of the circle.
• r is the radius of the circle.

The length of the arc that forms the sector's boundary can be calculated using:

                  Central Angle

  Arc Length= -------------- X 2πr

                       360∘

These formulas are derived from the fact that the area of a sector is proportional to the central angle it subtends and the entire area of the circle. Similarly, the length of the arc is proportional to the circumference of the circle and the central angle.