CLASS-6
DIAMETER, RADIUS, AND CHORD OF CIRCLE
DIAMETER, RADIUS, AND CHORD OF CIRCLE -
Chord Of A Circle -
A line segment joining any two points of a circle is called chord of the circle. In the below figure AB is the chord of the circle with centre C. The distance AB is called the length of the chord.
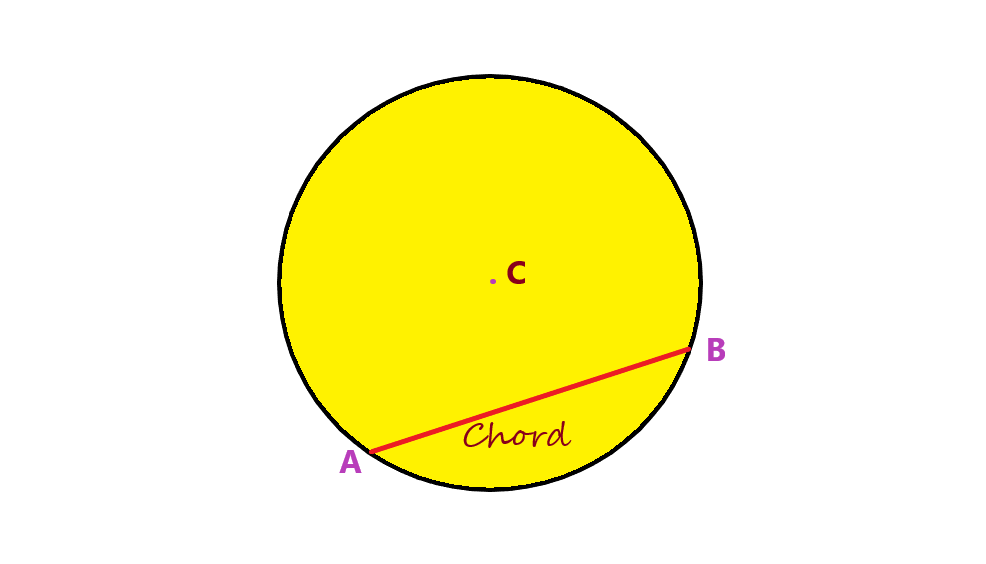
A chord of a circle is a straight line segment whose endpoints lie on the circumference (boundary) of the circle. In other words, it's a line segment that connects two points on the circle.
The length of a chord can vary, depending on its position and orientation relative to the circle.
The diameter of a circle is a special case of a chord; it is the longest chord of the circle because it passes through the center of the circle.
The length of a chord can be calculated using the distance formula if you know the coordinates of its endpoints. However, if you know the length of the chord and the distance from the center of the circle to the chord (which is called the "distance from the center to the chord" or the "chord's perpendicular distance"), you can also calculate the radius of the circle using the following formula:
r = √(d²/4 + h²)
Where:
- r is the radius of the circle.
- d is the length of the chord.
- h is the distance from the center of the circle to the chord.
This formula is derived from the Pythagorean theorem, where d/2 is the base of a right triangle formed by the radius, the chord, and the perpendicular distance. The hypotenuse of this triangle is the radius, and the height is the distance from the center to the chord.
Diameter -
The diameter of a circle is the distance across the circle passing through its center, and it is twice the length of the radius. If we denote the diameter as d and the radius as r, then the relationship between them is:
d = 2r
Conversely, if you have the diameter and want to find the radius, you can use the formula:
2r = d
Where:
- d is the diameter of the circle.
- r is the radius of the circle.
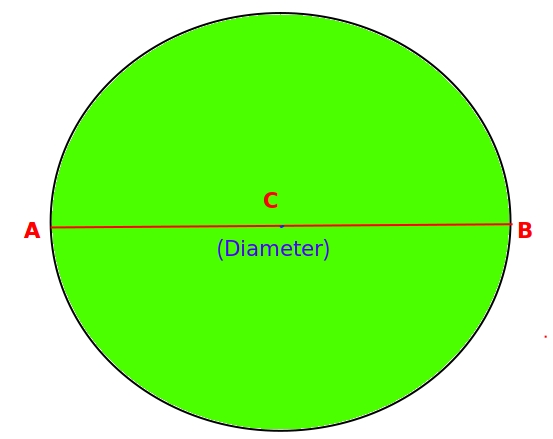
A chord of a circle passing through its centre is called a diameter of the circle. In the above figure AB is the diameter of the circle with centre D. Notice that, CA & CB are both radii of the circle, so CA = CB = r.
It follows that, AB = 2r = 2 X radius.
Thus -
Length of a Diameter = 2 X radius
Diameter is the longest chord of the circle.
Radius -
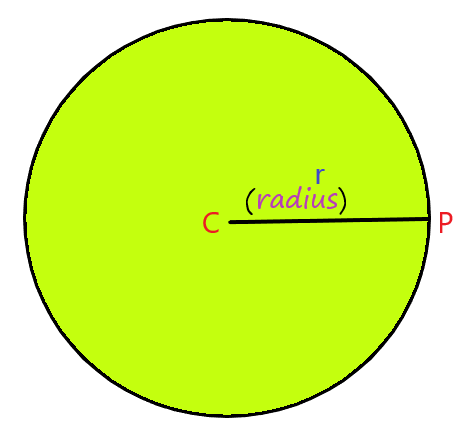
The radius of a circle is a line segment that joins the center of the circle to any point on the circle's circumference. It's essentially the distance from the center of the circle to any point on its edge.
If you know the diameter of the circle, you can find the radius by dividing the diameter by 2:
r = d/2
Conversely, if you know the circumference of the circle, you can find the radius using the formula:
r = C/2π
Where:
- r is the radius of the circle.
- d is the diameter of the circle.
- C is the circumference of the circle.
- π is a mathematical constant approximately equal to 3.14159.
If you know the area of the circle, you can find the radius using the formula:
r = √ A/π
Where:
- A is the area of the circle.
These formulas are fundamental in geometry and are used to calculate various properties of circles.