CLASS-6
ARC OF A CIRCLE

ARC OF A CIRCLE -

The arc of a circle refers to a portion of the circumference of a circle. It is a curved segment connecting two points on the circle, just like a piece of string stretched along the circumference between two points. The length of an arc is determined by the measure of the central angle subtended by the arc at the center of the circle and the radius of the circle.

The formula to calculate the length of an arc (s) in a circle is:

          s = r ⋅ θ

Where:

• s = arc length
• r = radius of the circle
• θ = central angle (in radians) subtended by the arc

Alternatively, if the central angle is given in degrees (θ∘), you can use the formula:

                      θ

           s = ---------- ⋅ 2πr

                    360

Where 2πr represents the circumference of the circle.

Other Way Of Understanding -

The arc of a circle is a segment of the circumference of a circle. It is formed by two points on the circle and the continuous portion of the circumference connecting these two points. The length of the arc can be calculated using the formula:

                                           Angle  

                        Arc Length = ----------- X 2πr

                                            360∘

Where:

• Arc Length is the length of the arc.
• Angle is the angle subtended by the arc at the centre of the circle (measured in degrees).
• r is the radius of the circle.

Alternatively, if the angle is given in radians (where 2π radians is equivalent to 360∘), the formula can be expressed as:

                     Arc Length = Angle × Arc Length = Angle × r

In this case, the angle is given in radians.

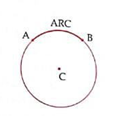
A continuous part of a circle is called an arc of the circle.

In the above diagram, AB is arc of the circle with centre C.