CLASS-6
ANGLE SUBTENDED BY AN ARC
ANGLE SUBTENDED BY AN ARC -
The angle subtended by an arc is the angle formed at the centre of a circle when two radii (lines from the centre to any two points on the circumference) are drawn to the endpoints of the arc. This angle is measured in degrees or radians, depending on the units used.
The measure of the angle is equal to the ratio of the arc length to the radius of the circle, multiplied by 360 degrees (or 2π radians for radian measure). The formula for calculating the angle (θ) subtended by an arc is:
θ = s/r × 360∘
where:
- θ is the angle in degrees,
- s is the arc length,
- r is the radius of the circle.
In radians, the formula is:
s
θ = ------
r
Keep in mind that for a full circle, the central angle is 360 degrees or 2π radians, and for a semicircle, it is 180 degrees or π radians.
If the angle is in degrees, you can use the formula:
s 180
θ = ------ × --------
r π
where, π ≈ 3.14159.
This formula comes from the definition of radians, where the arc length s is equal to the radius r when the angle θ is 1 radian.
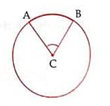
The angle formed by two radii of an arc of a circle at the centre of the circle is called the angle subtended by the arc.
In the above diagram, ∠ACB is the angle subtended by the arc AB of a circle with centre C.